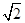题目内容
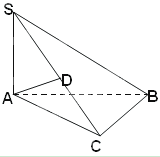
如图,在四棱锥 中,
中,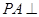 底面
底面 ,
, ,
, ,
,
 ,
, 是
是 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)证明: 平面
平面 ;
;
(Ⅲ)求二面角 的正切值.
的正切值.
 中,
中,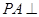 底面
底面 ,
, ,
, ,
,
 ,
, 是
是 的中点.
的中点.(Ⅰ)证明:
 ;
;(Ⅱ)证明:
 平面
平面 ;
;(Ⅲ)求二面角
 的正切值.
的正切值.
(Ⅰ)证明:见解析。(Ⅱ)证明:见解析。(Ⅲ)二面角 的正切值是
的正切值是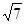 .
.
 的正切值是
的正切值是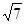 .
.试题分析:(1)根据题目中的线面的垂直性质定理得到线线垂直的证明。
(2)利用上一问的结论和线面垂直的判定定理得到证明。
(3)结合三垂线定理作出二面角的平面角,然后借助于三角形来求解大小。
(Ⅰ)证明:在四棱锥
 中,因
中,因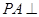 底面
底面 ,
,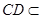 平面
平面 ,故
,故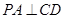 .
.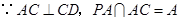 ,
,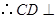 平面
平面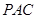 .
.而
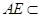 平面
平面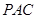 ,
,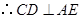 .…………………………………………(4分)
.…………………………………………(4分)(Ⅱ)证明:由
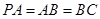 ,
,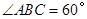 ,可得
,可得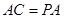 .
.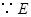 是
是 的中点,
的中点,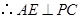 .
.由(Ⅰ)知,
 ,且
,且 ,所以
,所以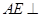 平面
平面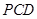 .
.而
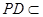 平面
平面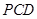 ,
,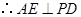 .
.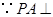 底面
底面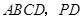 在底面
在底面 内的射影是
内的射影是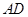 ,
,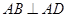 ,
, .
.又
 ,综上得
,综上得 平面
平面 .………………………………(8分)
.………………………………(8分)(Ⅲ)解法一:过点
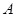 作
作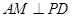 ,垂足为
,垂足为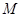 ,连结
,连结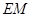 .则(Ⅱ)知,
.则(Ⅱ)知,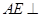 平面
平面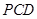 ,
,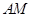 在平面
在平面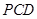 内的射影是
内的射影是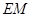 ,则
,则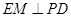 .
.因此
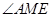 是二面角
是二面角 的平面角.
的平面角.由已知,得
 .设
.设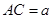 ,
,可得
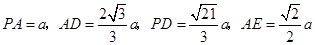 .
.在
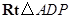 中,
中,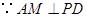 ,
,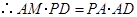 ,
,则
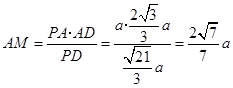 .
.在
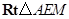 中,
中,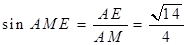 .
.所以二面角
 的正切值为
的正切值为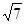 .……………………………………(12分)
.……………………………………(12分)解法二:由题设
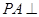 底面
底面 ,
, 平面
平面 ,则平面
,则平面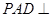 平面
平面 ,交线为
,交线为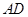 .
.过点
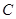 作
作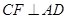 ,垂足为
,垂足为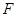 ,故
,故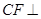 平面
平面 .过点
.过点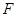 作
作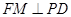 ,垂足为
,垂足为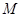 ,连结
,连结 ,故
,故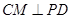 .因此
.因此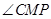 是二面角
是二面角 的平面角.
的平面角.由已知,可得
 ,设
,设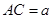 ,
,可得
 .
.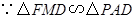 ,
, .
.于是,
 .
.在
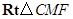 中,
中, .
.所以二面角
 的正切值是
的正切值是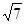 .
.(建立直角坐标系相应给分)
点评:解决该试题的关键是能合理的建立空间直角坐标系,表示出法向量以及直线的方向向量,借助于向量的知识来得到证明和求解,或者借助于线面的垂直的判定定理和性质定理得到结论。

练习册系列答案
相关题目
 .
.
 和矩形
和矩形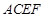 所在的平面互相垂直,
所在的平面互相垂直, ,
, ,
, 是线段
是线段 的中点.
的中点.
 //平面
//平面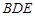 ;
; 的大小;
的大小; 上确定一点
上确定一点 ,使得
,使得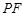 与
与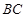 所成的角是
所成的角是 .
.

 .(
.( )
)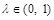 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF; ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 β,给出四个命题:( )
β,给出四个命题:( ) ,则点
,则点 与直线
与直线 的位置关系用符号表示为 ;
的位置关系用符号表示为 ; 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 ,且
,且 ,过
,过 ,则
,则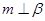

 ,CD
,CD ,AB⊥
,AB⊥ 于A,CD⊥
于A,CD⊥