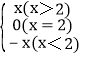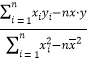Question

【题目】设a，b∈Z，若对任意x≤0，都有（ax+2）（x2+2b）≤0，则a+b=______．

Answer 1

【答案】-1

【解析】

根据题意，设f（x）=ax+2，g（x）=x2+2b，分析可得b＜0，结合二次函数的性质分析可得在（-∞，），g（x）＞0，在（，0），g（x）＜0；又由（ax+2）（x2+2b）≤0，分析可得对于f（x）=ax+2，在（-∞，），f（x）＜0，在（，0），f（x）＞0；进而可得有f（）=（-a）×+2=0，结合a，b∈Z，分析可得答案．

解：根据题意，设f（x）=ax+2，g（x）=x2+2b，

当b≥0时，g（x）=x2+2b≥0，而f（x）=ax+2≤0不可能在（-∞，0]上恒成立，

必有b＜0，

对于g（x）=x2+2b，b＜0，

在（-∞，），g（x）＞0，在（，0），g（x）＜0；

若（ax+2）（x2+2b）≤0，

则对于f（x）=ax+2，在（-∞，），f（x）＜0，在（，0），f（x）＞0；

而f（x）为一次函数，则必有f（）=（-a）×+2=0，且a＞0，

变形可得：a2（-b）=2，

又由a，b∈Z，则a=1，b=-2；

故a+b=-1；

故答案为：-1．