题目内容
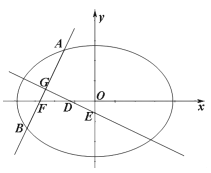
【题目】如图,椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,
两点,![]() 的最大值为
的最大值为![]() ,
,![]() 的最小值为
的最小值为![]() ,满足
,满足![]() .
.
(1)若线段![]() 垂直于轴时,
垂直于轴时,![]() ,求椭圆的方程;
,求椭圆的方程;
(2)设线段![]() 的中点为
的中点为![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点,记
是坐标原点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)依题意得![]() ,代入
,代入![]() ,结合
,结合![]() ,解方程组,可求得
,解方程组,可求得![]() 的值,即求得椭圆方程.(2)由(1)知
的值,即求得椭圆方程.(2)由(1)知![]() ,由此设出椭圆方程为
,由此设出椭圆方程为![]() ,设出直线
,设出直线![]() 的方程并代入椭圆的方程,写出韦达定理,并写出
的方程并代入椭圆的方程,写出韦达定理,并写出![]() 点的坐标,利用
点的坐标,利用![]() 求得
求得![]() 点的横坐标,列出面积的表达式并化简,由此求得面积比的取值范围.
点的横坐标,列出面积的表达式并化简,由此求得面积比的取值范围.
解:(1)设![]() ,则椭圆性质得:
,则椭圆性质得:
![]() ,
,![]() ,而
,而![]() ,
,
![]() 有
有![]() ,即
,即![]() ,
,![]() ,
,
又![]() 且
且![]() ,得
,得![]() ,
,![]() ,
,
因此椭圆的方程为:![]() .
.
(2)由(1)可知![]() ,
,![]() ,椭圆的方程为
,椭圆的方程为![]() .
.
由题意知直线![]() 的斜率一定存在不为零,设直线
的斜率一定存在不为零,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,则由
,则由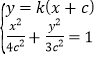 消去
消去![]() 并整理得
并整理得![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
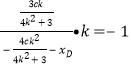 ,
,
![]() .
.
由![]() 与
与![]() 相似得
相似得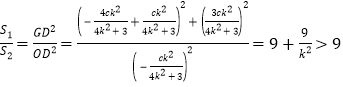 .
.
故![]() 的取值范围为
的取值范围为![]() .
.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:
(单位:![]() )的影响,对近
)的影响,对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量
和年销售量![]() 作了初步统计和处理,得到的数据如下:
作了初步统计和处理,得到的数据如下:
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
![]() ,
,![]() .
.

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若公司计划下一年度投入宣传费![]() 万元,试预测年销售量
万元,试预测年销售量![]() 的值.
的值.
参考公式
【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01
