Question

给一个正方体的六个面涂上四种不同颜色（红、黄、绿、蓝），要求相邻两个面涂不同的颜色，则共有涂色方法（　　）（涂色后，任意翻转正方体，能使正方体各面颜色一致，我们认为是同一种涂色方法）

A．6种

B．12种

C．24种

D．48种

Answer 1

A

试题分析：由于涂色过程中，要保证满足条件（用四种颜色，相邻的面不同色），正方体的三对面，必然有两对同色，一对不同色，而且三对面具有“地位对等性”，因此，只需从四种颜色中选择2种涂在其中一对面上，剩下的两种颜色涂在另外两个面即可。因此共有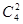=6种不同的涂法。选A.
点评：主要是考查了分步计数原理的运用，属于基础题。