题目内容
(本小题满分12分)
设函数 其中
其中 .
.
(Ⅰ)证明: 是
是 上的减函数;
上的减函数;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
设函数
 其中
其中 .
.(Ⅰ)证明:
 是
是 上的减函数;
上的减函数;(Ⅱ)若
 ,求
,求 的取值范围.
的取值范围.(1)利用函数单调性定义,设变量,作差,变形,定号,得到结论。
(2)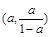
(2)
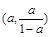
试题分析:(Ⅰ)设

则
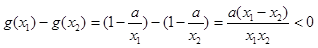
 又
又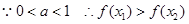
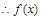 在
在 上是减函数························· 6分
上是减函数························· 6分(Ⅱ)
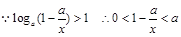 ····················· 8分
····················· 8分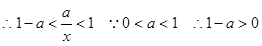 从而
从而 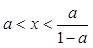 ········ 10分
········ 10分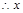 的取值范围是
的取值范围是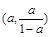 ·························· 12分
·························· 12分点评:函数单调性的证明一般用定义法。先设变量,作差(或作商),变形,定号,下结论。
同时对于含有参数的对数不等式的求解,底数不定要分类讨论,属于中档题。

练习册系列答案
相关题目
 ,则满足不等式
,则满足不等式 的x的范围是( )
的x的范围是( )

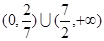

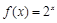 及函数
及函数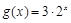 的图象分别相交于A,B两点,则
的图象分别相交于A,B两点,则
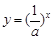 ,当
,当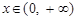 时,有
时,有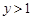 ,解关于x的不等式
,解关于x的不等式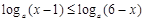
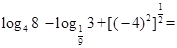 _____________.
_____________. ,则( )
,则( ) B.
B. 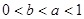
 D.
D. 
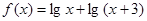 的定义域为 .
的定义域为 .