Question

10．如图所示，在三棱锥D-ABC中，AB=BC=CD=1，AC=$\sqrt{3}$，平面ACD⊥平面ABC，∠BCD=90°．
（Ⅰ）求证：CD⊥平面ABC；
（Ⅱ）求直线BC与平面ABD所成角的正弦值．

Answer 1

分析 （I）取AC中点M，连结BM，过M在平面ACD上作MN⊥AC，通过已知条件可分别以MB、MC、MN为x、y、z轴建立空间直角坐标系，设D（0，y，z），利用∠BCD=90°即$\overrightarrow{BC}$•$\overrightarrow{CD}$=0，可得D（0，$\frac{\sqrt{3}}{2}$，1），进而CD⊥平面ABC；
（II）通过题意，直线BC与平面ABD所成角的正弦值即为平面ABD的法向量与$\overrightarrow{BC}$的夹角的余弦值的绝对值，计算即可．

解答 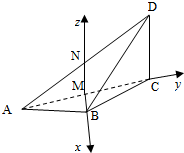解：（I）取AC中点M，连结BM，过M在平面ACD上作MN⊥AC，
∵平面ACD⊥平面ABC，∴MN⊥平面ABC，
又∵AB=BC，∴MB⊥AC，
分别以MB、MC、MN为x、y、z轴建立空间直角坐标系如图，
则有B（$\frac{1}{2}$，0，0），C（0，$\frac{\sqrt{3}}{2}$，0），设D（0，y，z），
则有$\overrightarrow{BC}$=（$-\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0），$\overrightarrow{CD}$=（0，y-$\frac{\sqrt{3}}{2}$，z），
∵∠BCD=90°，∴$\overrightarrow{BC}$•$\overrightarrow{CD}$=0，解得y=$\frac{\sqrt{3}}{2}$，
又∵CD=1，∴D（0，$\frac{\sqrt{3}}{2}$，1），
∴$\overrightarrow{CD}$=（0，0，1），故CD⊥平面ABC；
（II）A（0，-$\frac{\sqrt{3}}{2}$，0），设平面ABD的法向量为$\overrightarrow{n}$=（x，y，z），
由$\overrightarrow{AD}$=（0，$\sqrt{3}$，1），$\overrightarrow{AB}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0），
得$\left\{\begin{array}{l}{\overrightarrow{AD}•\overrightarrow{n}=\sqrt{3}y+z=0}\\{\overrightarrow{AB}•\overrightarrow{n}=\frac{1}{2}x+\frac{\sqrt{3}}{2}y=0}\end{array}\right.$，取$\overrightarrow{n}$=（$-\sqrt{3}$，1，$-\sqrt{3}$），
又∵$\overrightarrow{BC}$=（$-\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0），
∴sinθ=|$cos＜\overrightarrow{BC}，\overrightarrow{n}＞$|=$\frac{\sqrt{3}}{\sqrt{7}•1}$=$\frac{\sqrt{21}}{7}$．

点评 本题考查线面垂直的判定定理，向量的数量积运算，注意解题方法的积累，属于中档题．