题目内容

3．方程cosx=lg|x|有6个根．

分析 根据y=cosx的图象和函数 y=lg|x|的图象在（0，+∞）上有3个交点，结合函数的图象关于y轴对称可得结论．

解答 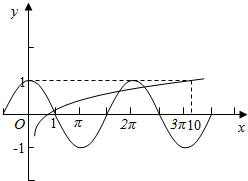解：函数y=cosx和函数 y=lg|x|都是偶函数，它们的图象关于y轴对称，
根据y=cosx的图象和函数 y=lg|x|的图象在（0，+∞）上有3个交点，
可得y=cosx的图象和函数 y=lg|x|的图象在R上有6个交点，即方程cosx=lg|x|有6个实数根，
故答案为：6．

点评 本题主要考查方程根的存在性以及个数判断，余弦函数的图象的特征，体现了数形结合、转化的数学思想，属于中档题．

练习册系列答案
相关题目
10．试比较下列各数的大小．
$（\frac{2}{3}）^{-\frac{1}{3}}$，$（\frac{3}{5}）^{\frac{1}{2}}$，${3}^{\frac{2}{3}}$，$（\frac{2}{5}）^{\frac{1}{2}}$，$（\frac{3}{2}）^{\frac{2}{3}}$，$（\frac{5}{6}）^{0}$，$（\frac{5}{3}）^{-\frac{2}{5}}$．
11．设f（x）=x2-2|x|-3，在下列直角坐标系中画出f（x）的图象．
11．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$，2（$\overrightarrow{a}$-$\overrightarrow{c}$）（$\overrightarrow{b}$-$\overrightarrow{c}$）=|$\overrightarrow{a}$-$\overrightarrow{c}$||$\overrightarrow{b}$-$\overrightarrow{c}$|，则|$\overrightarrow{c}$|的最大值为（　　）
A．2B．$\sqrt{3}$C．$\sqrt{2}$D．1
18．从某项综合能力测试中抽取100人的成绩，统计如下表，则这100人的成绩的方差为（　　）
（其中，s2=$\frac{1}{n}{\sum_{i=1}^n{（{x_i}-\overline x）}^2}$）
分数54321
人数2010303010
A．3B．$\frac{8}{5}$C．9D．$\frac{{2\sqrt{10}}}{5}$
8．已知f（x）是二次函数，且f（-1）=4，f（0）=1，f（3）=4．
（1）求f（x）的解析式．
（2）若x∈[-1，5]，求函数f（x）的值域．
15．在△ABC中，cosB=$\frac{12}{13}$，cosC=-$\frac{3}{5}$．
（Ⅰ）求sinA的值；    
（Ⅱ）设AC=5，求△ABC的面积．
12．在△ABC中，已知A=$\frac{π}{6}$，a=$\frac{{4\sqrt{3}}}{3}$，b=4，则角B=$\frac{π}{3}$或$\frac{2π}{3}$．
13．已知点A（1，-1），B（4，0），C（2，2），平面区域D由所有满足$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$（1＜λ≤a，1＜μ≤b）的点P（x，y）组成．若区域D的面积为8，则a+b的最小值为（　　）
A．$\frac{3}{2}$B．2C．4D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网