题目内容
17.已知角θ∈(0,2π),关于x的方程2x2-($\sqrt{3}$-1)x+m=0的两根为sinθ,cosθ.(1)求m的值;
(2)求方程的两根及此时θ的值.
分析 (1)由sinθ+cosθ=$\frac{\sqrt{3}-1}{2}$、sinθcosθ=$\frac{m}{2}$以及同角三角函数的基本关系可得 1+m=$\frac{2-\sqrt{3}}{2}$,由此解得m的值.
(2)由以上可得,sinθ+cosθ=$\frac{\sqrt{3}-1}{2}$、sinθcosθ=-$\frac{\sqrt{3}}{4}$,即可解得sinθ 和cosθ 的值,从而求得故此时方程的两个根及θ的值.
解答 解:(1)由sinθ+cosθ=$\frac{\sqrt{3}-1}{2}$、sinθcosθ=$\frac{m}{2}$,
∴sin2θ+2sinθcosθ+cos2θ=($\frac{\sqrt{3}-1}{2}$)2,即 1+m=$\frac{2-\sqrt{3}}{2}$,
解得 m=-$\frac{\sqrt{3}}{2}$.
(2)由以上可得,sinθ+cosθ=$\frac{\sqrt{3}-1}{2}$、sinθcosθ=-$\frac{\sqrt{3}}{4}$,
解得 sinθ=-$\frac{1}{2}$,cosθ=$\frac{\sqrt{3}}{2}$; 或者 sinθ=$\frac{\sqrt{3}}{2}$,cosθ=-$\frac{1}{2}$.
∵θ∈(0,2π),
∴θ=$\frac{11π}{6}$或$\frac{2π}{3}$.
点评 本题主要考查一元二次方程根与系数的关系,同角三角函数的基本关系的应用,三角函数的恒等变换,根据三角函数的值求角,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.已知数列{an}是等差数列,{bn}是正项等比数列,且a5=b6,则一定有( )
| A. | a3+a7≤b4+b8 | B. | a3+a7<b4+b8 | C. | a3+a7>b4+b8 | D. | a3+a7≥b4+b8 |
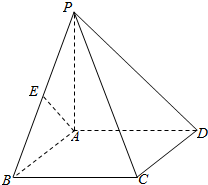 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点.求证:AE⊥PC.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点.求证:AE⊥PC.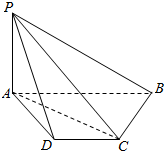 如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD=2,PA⊥平面ABCD,∠ABC=60°
如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD=2,PA⊥平面ABCD,∠ABC=60°