题目内容
2.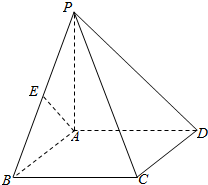 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点.求证:AE⊥PC.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点.求证:AE⊥PC.
分析 由已知得PA⊥AD,BA⊥AD,从而AD⊥平面PAB,进而BC⊥AE,再推导出AE⊥BP,由此能证明AE⊥PC.
解答 证明:∵PA⊥面ABCD,ABCD为矩形,
∴PA⊥AD,BA⊥AD,
∴AD⊥平面PAB,
∵AD∥BC,则BC⊥平面PAB,AE在平面PAB内,
∴BC⊥AE,
又∵E是棱PB的中点,PA=AB,
∴AE⊥BP,
∵BC和BP交于B点,
∴AE⊥面PBC,
∴AE⊥PC.
点评 本题考查异面直线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
1.设集合A={x|x≥3},B={x|x≤3},则A∩B=( )
| A. | ∅ | B. | R | C. | {x||x≤3} | D. | {3} |
10.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩B=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |
7.如图所示,三视图表示的几何体是( )
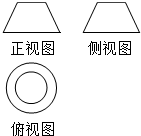

| A. | 圆台 | B. | 棱台 | C. | 棱柱 | D. | 圆锥 |
12.若函数y=x2-3x的定义域为{-1,0,2,3},则其值域为( )
| A. | {-2,0,4} | B. | {-2,0,2,4} | C. | $\left\{{\left.{y\left|{y≥}\right.-\frac{9}{4}}\right\}}\right.$ | D. | {y|0≤y≤3} |