Question

【题目】如图，正方体ABCD﹣A1B1C1D1的棱线长为1，线段B1D1上有两个动点E，F，且EF= ，则下列结论中错误的是（ ）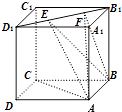
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE，BF所成的角为定值

Answer 1

【答案】D
【解析】解：∵在正方体中，AC⊥BD，∴AC⊥平面B1D1DB，BE平面B1D1DB，∴AC⊥BE，故A正确； ∵平面ABCD∥平面A1B1C1D1 ， EF平面A1B1C1D1 ， ∴EF∥平面ABCD，故B正确；
∵EF= ，∴△BEF的面积为定值 ×EF×1= ，又AC⊥平面BDD1B1 ， ∴AO为棱锥A﹣BEF的高，∴三棱锥A﹣BEF的体积为定值，故C正确；
∵利用图形设异面直线所成的角为α，当E与D1重合时sinα= ，α=30°；当F与B1重合时tanα= ，∴异面直线AE、BF所成的角不是定值，故D错误；
故选D．

利用证线面垂直，可证AC⊥BE；判断A正确；
根据正方体中上下面平行，由面面平行的性质可证，线面平行，从而判断B正确；
根据三棱锥的底面面积与EF的位置无关，高也与EF的位置无关，可判断C正确；
例举两个特除位置的异面直线所成的角的大小，根据大小不同判断D错误．