题目内容
椭圆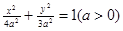 的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是 .
3a2
解析试题分析:设椭圆的右焦点为E.如图: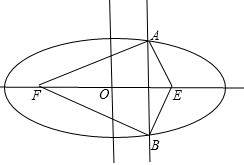
由椭圆的定义得:△FAB的周长:AB+AF+BF=AB+(4a-AE)+(4a-BE)=8a+AB-AE-BE;
∵AE+BE≥AB;
∴AB-AE-BE≤0,当AB过点E时取等号;
∴AB+AF+BF=8a+AB-AE-BE≤8a;
即直线x=m过椭圆的右焦点E时△FAB的周长最大;
此时△FAB的高为:EF=2a.
此时直线x=m=c=1;
把x=1代入椭圆的方程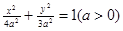 得:y=±
得:y=±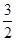 .
.
∴AB=3a.所以:△FAB的面积等于:S△FAB= ×3a×EF=
×3a×EF= ×3a×2a=3a2故答案为3a2
×3a×2a=3a2故答案为3a2
考点:本题主要考查椭圆的定义及几何性质,三角形面积计算。
点评:中档题,在解决涉及到圆锥曲线上的“焦点三角形”问题时,圆锥曲线的定义往往是解题的突破口.解决本题的关键在于利用定义求出周长的表达式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
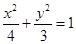 的右焦点
的右焦点 的直线交椭圆于于
的直线交椭圆于于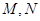 两点,令
两点,令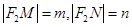 ,则
,则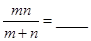 。
。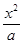 +
+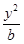 =1(
=1(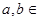 {1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .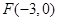 的距离比它到直线
的距离比它到直线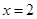 的距离大1,则点P满足的方程为 .
的距离大1,则点P满足的方程为 . 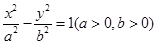 的一条渐近线方程是
的一条渐近线方程是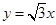 ,它的一个焦点在抛物线
,它的一个焦点在抛物线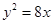 的准线上,则双曲线的方程为 .
的准线上,则双曲线的方程为 .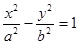 (a>0,b>0) 的焦点到渐近线的距离是a,则双曲线的离心率的值是 .
(a>0,b>0) 的焦点到渐近线的距离是a,则双曲线的离心率的值是 .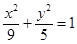 的中心为顶点,右焦点为焦点的抛物线方程是 .
的中心为顶点,右焦点为焦点的抛物线方程是 .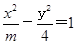 的右焦点与抛物线
的右焦点与抛物线 =12x的焦点重合,则m=______________.
=12x的焦点重合,则m=______________.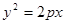 的焦点与双曲线
的焦点与双曲线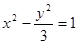 的右焦点重合,则
的右焦点重合,则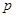 的值为 .
的值为 .