题目内容
已知直线l:y=| 1 |
| 2 |
| 5 |
| 4 |
分析:求出抛物线C:y2=2px(p>0)的顶点O关于直线l的对称点P(1,-2),再代入标准方程求出2p即求得方程.
解答:解:抛物点P(a,b),线C:y2=2px(p>0)的顶点O,设O关于直线l的对称点P(a,b),则有
解得
,
点P(a,b)在该抛物线上,所以4=2p.∴抛物线C的方程是y2=4x
|
|
点P(a,b)在该抛物线上,所以4=2p.∴抛物线C的方程是y2=4x
点评:本题考查抛物线标准方程求解,点关于直线的对称点的求解.属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
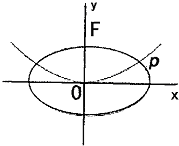 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: