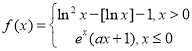题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(Ⅱ)当![]() 时,求证:过点
时,求证:过点![]() 恰有2条直线与曲线
恰有2条直线与曲线![]() 相切.
相切.
【答案】(I)![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】
(I)对f(x)求导,判断f′(x)的符号得出f(x)的单调性,根据单调性得出f(x)的最小值;(II)设过P的切线的切点为(x0,y0),根据导数的几何意义列出方程组,得出关于x0的方程,利用函数单调性证明此方程恰好有两解即可.
(Ⅰ)当a=3时,f(x)=x3﹣3x2,f'(x)=3x2﹣6x=3x(x﹣2).
当x∈[0,2]时,f'(x)≤0,
所以f(x)在区间[0,2]上单调递减.
所以f(x)在区间[0,2]上的最小值为f(2)=﹣4.
(Ⅱ)设过点P(1,f(1))的曲线y=f(x)的切线切点为(x0,y0),f'(x)=3x2﹣2ax,f(1)=1﹣a,
所以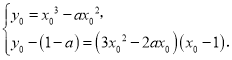
所以![]() .
.
令g(x)=2x3﹣(a+3)x2+2ax+1﹣a,
则g'(x)=6x2﹣2(a+3)x+2a=(x﹣1)(6x﹣2a),
令g'(x)=0得x=1或![]() ,
,
因为a>3,所以![]() .
.
x | (﹣∞,1) | 1 |
|
|
|
g′(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴g(x)的极大值为g(1)=0,g(x)的极小值为![]() ,
,
所以g(x)在![]() 上有且只有一个零点x=1.
上有且只有一个零点x=1.
因为g(a)=2a3﹣(a+3)a2+2a2+1﹣a=(a﹣1)2(a+1)>0,
所以g(x)在![]() 上有且只有一个零点.
上有且只有一个零点.
所以g(x)在R上有且只有两个零点.
即方程![]() 有且只有两个不相等实根,
有且只有两个不相等实根,
所以过点P(1,f(1))恰有2条直线与曲线y=f(x)相切.

 阅读快车系列答案
阅读快车系列答案【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与直线
与直线![]() 的直角坐标方程.
的直角坐标方程.
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下图是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”.
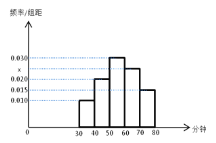
(1)求![]() 的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
(2)根据已知条件完成下面![]() 的列联表,并据此判断是否有
的列联表,并据此判断是否有![]() 的把握认为“读书谜”与性别有关?
的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 40 | ||
女 | 25 | ||
合计 |
附: ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
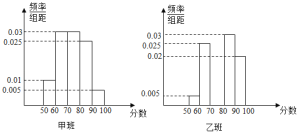
(1)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 总计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
总计 |
(2)从乙班![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: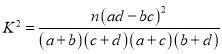 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
【题目】“一本书,一碗面,一条河,一座桥”曾是兰州的城市名片,而现在“兰州马拉松”又成为了兰州的另一张名片,随着全民运动健康意识的提高,马拉松运动不仅在兰州,而且在全国各大城市逐渐兴起,参与马拉松训练与比赛的人口逐年增加.为此,某市对人们参加马拉松运动的情况进行了统计调查.其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人,对其每周参与马拉松长跑训练的天数进行统计,得到以下统计表:
平均每周进行长跑训练天数 | 不大于2天 | 3天或4天 | 不少于5天 |
人数 | 30 | 130 | 40 |
若某人平均每周进行长跑训练天数不少于5天,则称其为“热烈参与者”,否则称为“非热烈参与者”.
(1)经调查,该市约有2万人参与马拉松运动,试估计其中“热烈参与者”的人数;
(2)根据上表的数据,填写下列2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关?
热烈参与者 | 非热烈参与者 | 合计 | |
男 | 140 | ||
女 | 55 | ||
合计 |
附:k2=![]() (n为样本容量)
(n为样本容量)
P(k2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |