题目内容
已知函数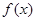 定义在
定义在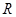 上,对任意的
上,对任意的 ,
,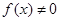 ,且
,且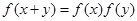 .
.
(1)求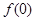 ,并证明:
,并证明: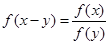 ;
;
(2)若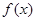 单调,且
单调,且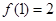 .设向量
.设向量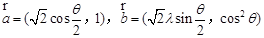 ,对任意
,对任意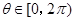 ,
, 恒成立,求实数
恒成立,求实数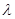 的取值范围.
的取值范围.
(1)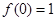 (2)
(2)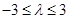
解析试题分析:(1)借助于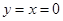 特殊值得
特殊值得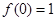 ,然后把
,然后把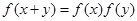 变形
变形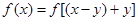 =
= 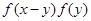 即可,(2) 首先判断出函数
即可,(2) 首先判断出函数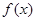 是增函数,然后找出
是增函数,然后找出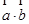 ,代入
,代入 整理的
整理的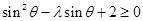 ,最后用分类讨论的思想方法求出
,最后用分类讨论的思想方法求出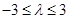 即可.
即可.
(1)令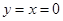 得
得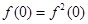 ,又∵
,又∵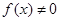 ,
,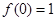 , 2分
, 2分
由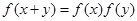 得
得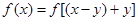 =
=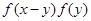 ,
,
∵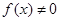 ,∴
,∴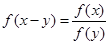 . 5分
. 5分
(2) ∵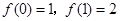 ,且
,且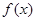 是单调函数,∴
是单调函数,∴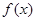 是增函数. 6分
是增函数. 6分
而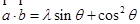 ,∴由
,∴由 ,得
,得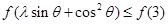 ,
,
又∵因为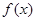 是增函数,∴
是增函数,∴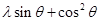
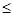
 恒成立,
恒成立,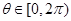 .
.
即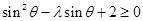 . 8分
. 8分
令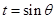 ,得
,得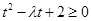 (﹡).
(﹡).
∵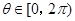 ,∴
,∴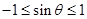 ,即
,即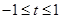 .
.
令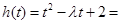
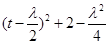
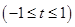 , 10分
, 10分
①当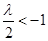 ,即
,即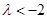 时,只需
时,只需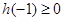 ,(﹡)成立,
,(﹡)成立,
∴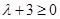 ,解得
,解得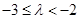 ; 11分
; 11分
②当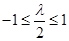 ,即
,即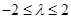 时,只需
时,只需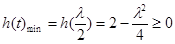 ,(﹡)成立,
,(﹡)成立,
∴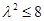 ,解得
,解得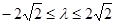 ,∴
,∴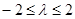 . 12分
. 12分
③当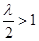 ,即
,即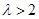 时,只需
时,只需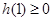 ,(﹡)成立,
,(﹡)成立,
∴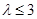 , ∴
, ∴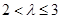 , 13分
, 13分
综上,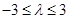 . 14分
. 14分
考点:抽象函数;函数的单调性;向量的数量积公式;不等式恒成立的问题;分类讨论的思想方法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
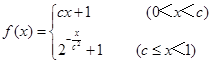 ,且
,且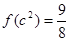 .
.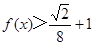 .
.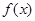 满足对任意的
满足对任意的 恒有
恒有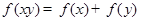 ,且当
,且当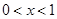 时,
时,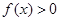 .
.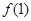 的值;
的值;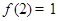 ,解不等式
,解不等式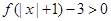 .
.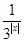 .
.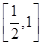 恒成立,求m的取值范围.
恒成立,求m的取值范围.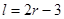 (
(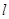 为圆柱的高,
为圆柱的高,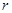 为球的半径,
为球的半径,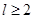 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为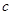 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.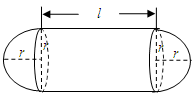
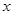 (单位:cm)满足关系:
(单位:cm)满足关系: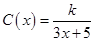 (
(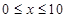 ,
,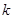 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设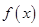 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.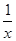 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.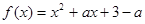 ,
,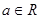 .
. 的取值范围,使
的取值范围,使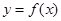 在闭区间
在闭区间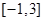 上是单调函数;
上是单调函数;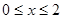 时,函数
时,函数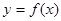 的最大值是关于
的最大值是关于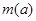 .求
.求
 ,恒有
,恒有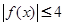 成立.
成立. .
.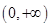 内的任意
内的任意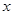 ,总有
,总有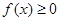 成立,求实数
成立,求实数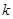 的取值范围;
的取值范围; 在区间
在区间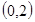 内有两个不同的零点
内有两个不同的零点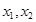 ,求:
,求: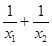 的取值范围.
的取值范围.