题目内容
【题目】一矩形的一边在![]() 轴上,另两个顶点在函数
轴上,另两个顶点在函数![]() 的图像上,如图,则此矩形绕
的图像上,如图,则此矩形绕![]() 轴旋转而成的几何体的体积的最大值是( )
轴旋转而成的几何体的体积的最大值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
用![]() 表示圆柱的体积可得
表示圆柱的体积可得![]() ,由基本不等式可求其最大值,从而得到正确的选项.
,由基本不等式可求其最大值,从而得到正确的选项.
因为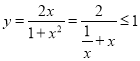 当且仅当
当且仅当![]() 时取等号,所以
时取等号,所以![]() .
.
因为矩形绕![]() 轴旋转一周旋转得到一个圆柱,
轴旋转一周旋转得到一个圆柱,
设![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
则圆柱的底面圆的半径为![]() ,高为
,高为![]() ,
,
因为![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以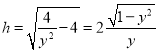 ,
,
所以圆柱得体积为![]() ,
,
当且仅当![]() 时取等号,
时取等号,
所以矩形绕![]() 轴旋转而成的几何体的体积的最大值是
轴旋转而成的几何体的体积的最大值是![]() ,
,
故选:A.
【点晴】
本题主要考查了空间几何体的体积的计算、基本不等式的应用,解答的关键确定![]() 的值,属于中档试题,同时着重考查了转化与化归的思想方法及数形结合的思想方法的应用,本题的解答中先求出
的值,属于中档试题,同时着重考查了转化与化归的思想方法及数形结合的思想方法的应用,本题的解答中先求出![]() 的范围,再设出点
的范围,再设出点![]() 的坐标,根据
的坐标,根据![]() 两点的纵坐标相等得到
两点的纵坐标相等得到![]() ,再求出高
,再求出高![]() ,根据图形旋转得到一个圆柱,根据圆柱的体积公式得到关系式,利用基本不等式求最值.
,根据图形旋转得到一个圆柱,根据圆柱的体积公式得到关系式,利用基本不等式求最值.

练习册系列答案
相关题目
【题目】下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯 | 户年用水量 (立方米) | 水价 | 其中 | ||
自来水费 | 水资源费 | 污水处理费 | |||
第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
第三阶梯 | 260以上 | 9.00 | 6.07 | ||
(Ⅰ)试写出水费![]() (元)与用水量
(元)与用水量![]() (立方米)之间的函数关系式;
(立方米)之间的函数关系式;
(Ⅱ)若某户居民年交水费1040元,求其中自来水费、水资源费及污水处理费各是多少?