题目内容
(2012•成都一模)设正方体ABC-A1B1C1D1 的棱长为2,动点E,F在棱A1B1上,动点P、Q分别在棱AD、CD上,若EF=1,A1E=x,DQ=y,DP=z(x,y,z>0),则下列结论中错误的是( )
分析:由线面平行的判定定理,得A项正确;由二面角的定义和正方体性质,可得B项没有错误;由线面垂直的判定与性质,可得D项也正确.根据锥体体积公式和正方体的性质,可得C项中三棱锥P-EFQ的体积与x、y大小无关,与z大小有关,故C项有错误,由此即可得到本题的答案.
解答:解: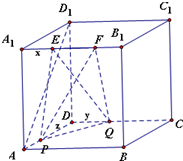 对于A,因为平面DPQ外一直线EF平行于平面DPQ内的直线DQ,
对于A,因为平面DPQ外一直线EF平行于平面DPQ内的直线DQ,
故EF∥平面DPQ,得A项正确;
对于B,当P点在AD上,由靠近点D的位置向A移动的过程中,
二面角P-EF-Q的大小逐渐增大,直到当P与A重合时,
二面角大小等于二面角A-A1B1-D,刚好等于
,故B正确;
对于C,由点Q到EF的距离等于2
,而EF=1,故S△EFQ=
不变,
而随着P在AD上运动,P到平面EFQ的距离为变量,从而使得三棱锥P-EFQ的
体积跟着变化,所以三棱锥P-EFQ的体积与x、y大小无关,与z大小有关,
由此可得C项有错误;
对于D,由线面垂直的判定定理,可得AD1⊥平面A1DCB1,而直线EQ在平面内运动,
可得不论EQ怎样运动,总有EQ与AD1成90°的角,与x、y的变化无关,故D项正确.
故选:C
 对于A,因为平面DPQ外一直线EF平行于平面DPQ内的直线DQ,
对于A,因为平面DPQ外一直线EF平行于平面DPQ内的直线DQ,故EF∥平面DPQ,得A项正确;
对于B,当P点在AD上,由靠近点D的位置向A移动的过程中,
二面角P-EF-Q的大小逐渐增大,直到当P与A重合时,
二面角大小等于二面角A-A1B1-D,刚好等于
| π |
| 4 |
对于C,由点Q到EF的距离等于2
| 2 |
| 1 |
| 2 |
| 2 |
而随着P在AD上运动,P到平面EFQ的距离为变量,从而使得三棱锥P-EFQ的
体积跟着变化,所以三棱锥P-EFQ的体积与x、y大小无关,与z大小有关,
由此可得C项有错误;
对于D,由线面垂直的判定定理,可得AD1⊥平面A1DCB1,而直线EQ在平面内运动,
可得不论EQ怎样运动,总有EQ与AD1成90°的角,与x、y的变化无关,故D项正确.
故选:C
点评:本题给出正方体中的动点,探索了线面位置关系、二面角的大小和锥体的体积,着重考查了空间角大小的求法、线面平行和线面垂直的证明等知识点,属于中档题.

练习册系列答案
相关题目