题目内容
二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,求实数m的取值范围
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,求实数m的取值范围
(1)f(x)=x2-x+1,(2)

试题分析:(1)求二次函数解析式,一般方法为待定系数法.二次函数解析式有三种设法,本题设一般式f(x)=ax2+bx+1,再利用等式恒成立,求出项的系数.由a(x+1)2+b(x+1)-ax2-bx=2x得2ax+a+b=2x,所以
 .(2)恒成立问题一般转化为最值问题.先构造不等式
.(2)恒成立问题一般转化为最值问题.先构造不等式 ,再变量分离
,再变量分离 ,这样就转化为求函数
,这样就转化为求函数 的最小值问题.
的最小值问题.试题解析:(1)设f(x)=ax2+bx+1
 a(x+1)2+b(x+1)-ax2-bx=2x
a(x+1)2+b(x+1)-ax2-bx=2x2ax+a+b=2x


 f(x)=x2-x+1
f(x)=x2-x+1(2)


考点:二次函数解析式,二次函数最值,不等式恒成立

练习册系列答案
相关题目
 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和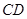 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 ,高
,高 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大 是定义在
是定义在 上的函数,且对任意实数
上的函数,且对任意实数 ,恒有
,恒有 ,且
,且 的解集为 .
的解集为 . (
( 为实常数).
为实常数). 在区间
在区间 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数 ,若不等式
,若不等式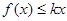 在
在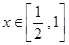 有解,求
有解,求 的取值范围.
的取值范围. 满足:对定义域内的任意
满足:对定义域内的任意 ,都有
,都有 ,则函数
,则函数



 ,若
,若 ,则
,则 的值为 .
的值为 .