题目内容
已知点 在圆
在圆 上运动,则
上运动,则 的最大值与最小值为( )
的最大值与最小值为( )
A. , , | B. | C.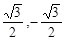 | D. |
A
解析试题分析:根据动点P在圆上运动,可知
表示的最大值和最小值为定点(2,1)与圆上点的斜率的取值范围。
设过点(2,1)的直线的斜率为k ,那么可知直线方程为y-1=k(x-2)
那么利用圆心到直线的距离为圆的半径,可知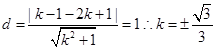
那么结合倾斜角和斜率的关系可知,最大值和最小值分别是 ,
, ,选A.
,选A.
考点:本试题考查了斜率几何意义的运用。
点评:解决该试题的关键是理解分式表示的意义是圆上的动点与定点(2,1)的两点的斜率 范围。然后结合圆的方程,结合数形结合思想得到结论,属于中档题。

练习册系列答案
相关题目
实数 ,
,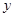 满足不等式组
满足不等式组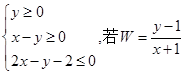 ,则有( ).
,则有( ).
A.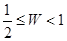 | B.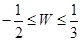 | C.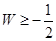 | D.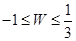 |
点 和点
和点 在直线
在直线 的两侧,则
的两侧,则 的取值范围是( )
的取值范围是( )
A. 或 或 | B. | C. 或 或 | D. |
设x,y满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的最大值是12,则
,若目标函数z=ax+by(a>0,b>0)的最大值是12,则 的最小值为( ).
的最小值为( ).
A. | B. | C. | D.4 |
若实数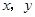 满足
满足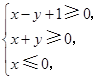 则
则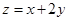 的最小值是( )
的最小值是( )
| A.0 | B.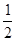 | C.1 | D.2 |
实数 ,
, 满足条件
满足条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )
| A.10 | B.12 | C.14 | D.15 |
某所学校计划招聘男教师x名,女教师y名,x和y须满足约束条件 则该校招聘的教师人数最多是( )
则该校招聘的教师人数最多是( )
| A.10 | B.8 | C.6 | D.12 |
已知 a,b满足a+2b=1,则直线ax+3y+b=0必过定点( )
A. | B. |
C. | D. |
已知x,y满足线性约束条件 ,则的取值范围是
,则的取值范围是
A. | B. | C. | D.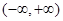 |