题目内容
函数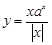
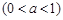 的图象的大致形状是 ( )
的图象的大致形状是 ( )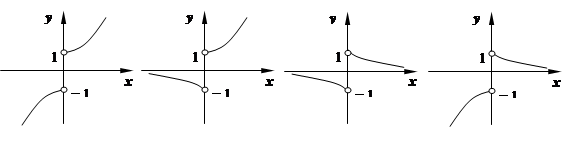
A. B. C. D.
D
解析试题分析:根据函数解析式,去掉绝对值符号得到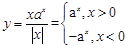 ,那么结合指数函数底数的范围可知,两段函数在定义域内是先增后减,故排除A,,B,C.因此可知选D.
,那么结合指数函数底数的范围可知,两段函数在定义域内是先增后减,故排除A,,B,C.因此可知选D.
考点:函数图像
点评:解决该试题的关键是要通过其性质和定义域和值域的范围来得到,属于基础题。

练习册系列答案
相关题目
设f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f( )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )
A. <x<1 <x<1 | B.x>2 |
C.x>2或 <x<1 <x<1 | D. <x<1或1<x<2 <x<1或1<x<2 |
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ,在
,在 上所有零点之和为( )
上所有零点之和为( )
| A.7 | B.8 | C.9 | D.10 |
下列函数中,既是奇函数又是区间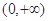 上的增函数的是( )
上的增函数的是( )
A.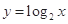 | B.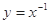 | C.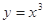 | D.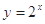 |
对于正实数 ,记
,记 为满足下述条件的函数
为满足下述条件的函数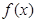 构成的集合:
构成的集合: 且
且 ,有
,有 .下列结论中正确的是
.下列结论中正确的是
A.若 ,则 ,则 |
B.若 且 且 ,则 ,则 |
C.若 ,则 ,则 |
D.若 且 且 ,则 ,则 |
若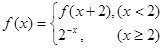 , 则
, 则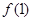 的值为
的值为 ( )
( )
| A.8 | B.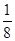 | C.2 | D.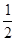 |
定义域为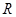 的函数
的函数 对任意
对任意 都有
都有 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )
A. | B. |
C. | D. |
若定义在R上的偶函数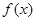 满足
满足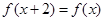 ,且当
,且当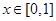 时,
时,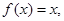 则方程
则方程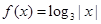 的解个数是 ( )
的解个数是 ( )
| A.0个 | B.2个 | C.4个 | D.6个 |
设函数 为定义在R上的奇函数,当
为定义在R上的奇函数,当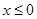 时,
时, (
( 为常数),则
为常数),则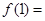 ( )
( )
| A.3 | B.1 | C.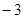 | D. |