题目内容
下列函数中,既是奇函数又是区间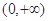 上的增函数的是( )
上的增函数的是( )
A.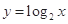 | B.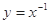 | C.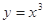 | D.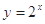 |
C
解析试题分析:对于A:由于函数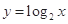 ,定义域不关于原点对称,因此是非奇非偶函数
,定义域不关于原点对称,因此是非奇非偶函数
对于B,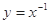 由于反比例函数是奇函数,但是在
由于反比例函数是奇函数,但是在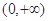 上是减函数,因此错误
上是减函数,因此错误
对于C,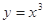 定义域为R,定义域内为增函数,且是奇函数,满足f(-x)=-f(x),成立。
定义域为R,定义域内为增函数,且是奇函数,满足f(-x)=-f(x),成立。
对于D, 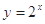 定义域关于原点对称,不满足f(x)=-f(-x),因此错误,故选C.
定义域关于原点对称,不满足f(x)=-f(-x),因此错误,故选C.
考点:函数的奇偶性和单调性
点评:解决的关键是熟练的掌握常见基本初等函数的 性质,属于基础题。

练习册系列答案
相关题目
已知¦(x)是实数集R上的奇函数,且在(0,+∞)上单调递增,若¦( )=0,三角形的一个锐角A满足¦(
)=0,三角形的一个锐角A满足¦(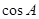 )<0,则A的取值范围是( )
)<0,则A的取值范围是( )
A.(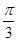 , ,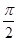 ) ) | B.(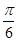 , ,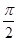 ) ) | C.(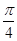 , ,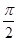 ) ) | D.(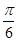 , ,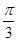 ) ) |
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1.5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
 的一个近似根(精确到0.1)为( )
的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5
设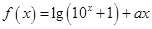 是偶函数,那么
是偶函数,那么 的值为( )
的值为( )
| A.1 | B.-1 | C.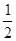 | D.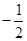 |
函数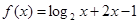 的零点必落在区间 ( )
的零点必落在区间 ( )
A.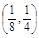 | B.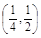 | C.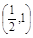 | D.(1,2) |
函数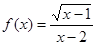 的定义域为( )
的定义域为( )
| A.[1,2)∪(2,+∞) | B.(1,+∞) | C.[1,2) | D.[1,+∞) |
已知函数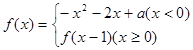 ,且函数
,且函数 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数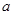 的取值范围是
的取值范围是
A. | B. | C.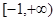 | D.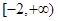 |


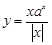
 的图象的大致形状是 ( )
的图象的大致形状是 ( )