题目内容
设f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f( )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )
A. <x<1 <x<1 | B.x>2 |
C.x>2或 <x<1 <x<1 | D. <x<1或1<x<2 <x<1或1<x<2 |
C
解析试题分析:因为f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f( )=0,所以当
)=0,所以当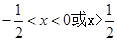 时,f(x)>0,所以由f(log4x)>0得
时,f(x)>0,所以由f(log4x)>0得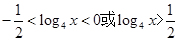 ,解得x>2或
,解得x>2或 <x<1。因此选C。
<x<1。因此选C。
考点:函数的奇偶性;函数的单调性;对数函数的单调性;对数不等式的解法。
点评:奇偶函数不等式求解时,要注意到:奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反。此题就是根据此条性质,数形结合来做的。

练习册系列答案
相关题目
已知函数 (
(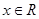 )满足
)满足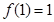 ,且
,且 的导函数
的导函数 <
<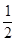 ,则
,则 <
<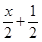 的解集为( )
的解集为( )
A.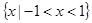 | B.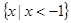 | C.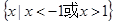 | D.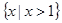 |
已知¦(x)是实数集R上的奇函数,且在(0,+∞)上单调递增,若¦( )=0,三角形的一个锐角A满足¦(
)=0,三角形的一个锐角A满足¦(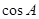 )<0,则A的取值范围是( )
)<0,则A的取值范围是( )
A.(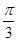 , ,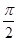 ) ) | B.(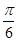 , ,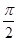 ) ) | C.(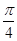 , ,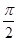 ) ) | D.(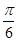 , ,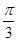 ) ) |
下列函数中,既是奇函数又是增函数的为( )
A. | B. | C. | D. |
定义在R上的函数 ,则
,则 的图像与直线
的图像与直线 的交点为
的交点为 、
、 、
、 且
且 ,则下列说法错误的是( )
,则下列说法错误的是( )
A. | B. |
C. | D. |
已知a是函数 的零点,
的零点, a,则
a,则 的值满足( )
的值满足( )
A. =0 =0 | B. >0 >0 | C. <0 <0 | D. 的符号不确定 的符号不确定 |
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1.5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
 的一个近似根(精确到0.1)为( )
的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5
 的部分图象,其中
的部分图象,其中 ,则下列所给图象中可能正确的是 ( )
,则下列所给图象中可能正确的是 ( )
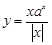
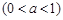 的图象的大致形状是 ( )
的图象的大致形状是 ( )