题目内容
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,∠ACB=90°,D是AB中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,∠ACB=90°,D是AB中点.(1)求证AC1∥平面CDB1;
(2)求异面直线AC1与B1C所成角的大小(用反三角表示)
分析:解法一:(1)要证B1C1∥平面EFG,只要在平面EFG内找出一直线与B1C1平行,由E,F为△AB,AC中点,可得GE∥BC.而B1C1∥BC,可得B1C1∥GE,从而可证
(2)由(1)知DO∥AC1,∠COD就是异面直线AC1与B1C所成的角.利用余弦定理求异面直线AC1与B1C所成角的余弦值;
解法二:利用空间向量法.如图建立坐标系,
(1)先求出平面CDB1的一个法向量,证得向量点积为零即得垂直,又AC1不在平面CDB1内,从而得出AC1∥平面CDB1
(2)先求得
=(-3,0,4),
=(0,-4,-4),利用向量的夹角公式求得两向量的夹角即可.
(2)由(1)知DO∥AC1,∠COD就是异面直线AC1与B1C所成的角.利用余弦定理求异面直线AC1与B1C所成角的余弦值;
解法二:利用空间向量法.如图建立坐标系,
(1)先求出平面CDB1的一个法向量,证得向量点积为零即得垂直,又AC1不在平面CDB1内,从而得出AC1∥平面CDB1
(2)先求得
| AC1 |
| B1C |
解答:解一:(1)证明:
连BC1交B1C于E,连DE
∵矩形BCC1B1中,E为BC1中点
又D为AB中点
∴DE
AC1
∵AC1在平面CDB1外,DE?平面CDB1
∴AC1∥平面CDB1
(2)∵AC1∥DE
∴∠CED或其补角为异面直线
AC1与B1C所成角
又CD=
,DE=
,CE=2
∴cos∠CED=
=
∴∠CED=arccos
.
解二:向量方法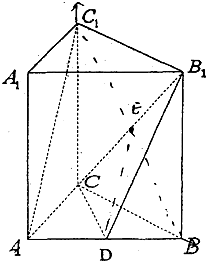
(1)如图,建系
A(3,0,0)B(0,4,0)C(10,0,0)
A1(3,0,4)B1(0,4,4)C1(10,0,4)D(
,2,0)
=(-3,0,4)
平面CDB1的一个法向量
=(4,-3,3),∵
•
=0,∴
⊥
又AC1不在平面CDB1内
∴AC1∥平面CDB1
(2)
=(-3,0,4),
=(0,-4,-4),cos?=
=-
∴cosθ=
,θ=arccos
连BC1交B1C于E,连DE
∵矩形BCC1B1中,E为BC1中点
又D为AB中点
∴DE
| ||
. |
| 1 |
| 2 |
∵AC1在平面CDB1外,DE?平面CDB1
∴AC1∥平面CDB1
(2)∵AC1∥DE
∴∠CED或其补角为异面直线
AC1与B1C所成角
又CD=
| 5 |
| 2 |
| 5 |
| 2 |
| 2 |
∴cos∠CED=
| CE2+DE2-CD2 |
| 2CE•PE |
| 2 |
| 5 |
| 2 |
∴∠CED=arccos
| 2 |
| 5 |
| 2 |
解二:向量方法

(1)如图,建系
A(3,0,0)B(0,4,0)C(10,0,0)
A1(3,0,4)B1(0,4,4)C1(10,0,4)D(
| 3 |
| 2 |
| AC1 |
平面CDB1的一个法向量
| n |
| AC1 |
| n |
| AC1 |
| n |
又AC1不在平面CDB1内
∴AC1∥平面CDB1
(2)
| AC1 |
| B1C |
| -16 | ||
5•4
|
| 2 |
| 5 |
| 2 |
∴cosθ=
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
点评:本题考查直线与平面的平行的判定,异面直线所成的角,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目




