题目内容
在Rt△ABC中,AC=3,BC=4,点D是斜边AB上的一点,且AC=AD.
(Ⅰ)求CD的长;
(Ⅱ)求sin∠BDC的值.
(Ⅰ)求CD的长;
(Ⅱ)求sin∠BDC的值.
分析:(I)在直角△ABC中,求得cosA=
,在△ACD中,根据余弦定理CD2=AC2+AD2-2AC•ADcosA,即可求CD的长;
(II)在△BCD中,求得sinB=
,根据正弦定理
=
,可求sin∠BDC的值.
| 3 |
| 5 |
(II)在△BCD中,求得sinB=
| 3 |
| 5 |
| BC |
| sin∠BDC |
| CD |
| sin∠B |
解答:解:(I)因为在直角△ABC中,AC=3,BC=4,所以AB=5,…(1分)
所以cosA=
…(3分)
在△ACD中,根据余弦定理CD2=AC2+AD2-2AC•ADcosA…(6分)
所以CD2=32+32-2•3•3•
所以CD=
…(8分)
(II)在△BCD中,sinB=
…(9分)
根据正弦定理
=
…(12分)
把BC=4,CD=
代入,得到sin∠BDC=
…(13分)
所以cosA=
| 3 |
| 5 |
在△ACD中,根据余弦定理CD2=AC2+AD2-2AC•ADcosA…(6分)
所以CD2=32+32-2•3•3•
| 3 |
| 5 |
所以CD=
6
| ||
| 5 |
(II)在△BCD中,sinB=
| 3 |
| 5 |
根据正弦定理
| BC |
| sin∠BDC |
| CD |
| sin∠B |
把BC=4,CD=
6
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查解三角形,考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
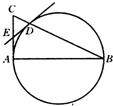 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.