题目内容
二次函数f（x）=ax2+bx+c，（a是正整数），c≥1，a+b+c≥1，方程ax2+bx+c=0有两个小于1的不等正根，则a的最小值为（ ）A．2
B．3
C．4
D．5
【答案】分析：将二次函数f（x）设成两根式形式，根据条件写出两根式形式的关系式，将a分离出来，然后利用基本不等式求出最值即可
解答：解：设f（x）=a（x-p）（x-q），其中p，q属于（0，1）且p不等于q．
由f（0）≥1及f（1）≥1，可得：apq≥1，a（1-p）（1-q）≥1，
两式相乘有a2p（1-p）q（1-q）≥1，即a2≥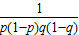
，
又由基本不等式可得：p（1-p）q（1-q）≤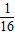
由于上式取等号当且仅当p=q=
与已知矛盾，故上式的等号取不到，
故p（1-p）q（1-q）＜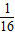
因此得到a2＞16即a＞4
所以函数f（x）=5x2-5x+1满足题设的所有条件，
因此a的最小值为5．
故选D．
点评：本题主要考查了函数与方程的综合运用，以及根的分布问题，本题解题的关键是熟练应用基本不等式求最值，属于中档题目．
解答：解：设f（x）=a（x-p）（x-q），其中p，q属于（0，1）且p不等于q．
由f（0）≥1及f（1）≥1，可得：apq≥1，a（1-p）（1-q）≥1，
两式相乘有a2p（1-p）q（1-q）≥1，即a2≥
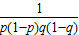，又由基本不等式可得：p（1-p）q（1-q）≤
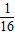
由于上式取等号当且仅当p=q=
与已知矛盾，故上式的等号取不到，故p（1-p）q（1-q）＜
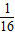
因此得到a2＞16即a＞4
所以函数f（x）=5x2-5x+1满足题设的所有条件，
因此a的最小值为5．
故选D．
点评：本题主要考查了函数与方程的综合运用，以及根的分布问题，本题解题的关键是熟练应用基本不等式求最值，属于中档题目．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
+bx（ａ，ｂ是常数且ａ
０）满足条件：ｆ（２）＝０．方程ｆ（ｘ）＝ｘ有等根