题目内容
(本题满分13分)
某俱乐部举行迎圣诞活动,每位会员交50元活动费,可享受20元的消费,并参加一次游戏:掷两颗正方体骰子,点数之和为12点获一等奖,奖价值为a元的奖品;点数之和为11或10点获二等奖,奖价值为100元的奖品;点数之和为9或8点获三等奖,奖价值为30元的奖品;点数之和小于8点的不得奖。求:
(1)同行的两位会员中一人获一等奖、一人获二等奖的概率;
(2)如该俱乐部在游戏环节不亏也不赢利,求a的值。
(1)P(A)=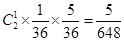 ;
(2)一等奖可设价值为310 元的奖品。
;
(2)一等奖可设价值为310 元的奖品。
【解析】
试题分析:(Ⅰ)设掷两颗正方体骰子所得的点数记为(x,y),其中1≤x,y≤6,则获
一等奖只有(6,6)一种可能,获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,由此能求出同行的三位会员一人获一等奖、两人获二等奖的概率.
(Ⅱ)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为30-a,-70,0,30,分别求
出P(ξ=30-a),P(ξ=-70),P(ξ=0),P(ξ=30)的值,由此能求出ξ的分布列和
Eξ.
解:(1)设掷两颗正方体骰子所得的点数记为(x,y),其中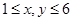 ,
,
则获一等奖只有(6,6)一种可能,其概率为: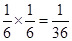 ; …………2分
; …………2分
获二等奖共有(6,5)、(5,6)、(4,6)、(6,4)、(5,5)共5种可能,其概率为: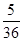 ;
;
…………5分
设事件A表示“同行的两位会员中一人获一等奖、一人获二等奖”,则有:
P(A)=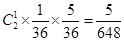 ;
…………6分
;
…………6分
(2)设俱乐部在游戏环节收益为ξ元,则ξ的可能取值为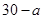 ,
,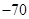 ,0,
,0,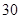 ,……7分
,……7分
|
ξ |
30-a |
-70 |
0 |
30 |
|
p |
|
|
|
|
其分布列为:
则:Eξ=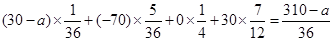 ;
…………11分
;
…………11分
由Eξ=0得:a=310,即一等奖可设价值为310 元的奖品。 …………13分
考点:本试题主要考查了离散型随机变量的分布列和数学期望.
点评:解决该试题的关键是解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
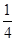
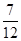
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.