题目内容
如图,在平面直角坐标系 中,以
中,以 轴为始边,两个锐角
轴为始边,两个锐角 ,
, 的终边分别与单位圆相交于A,B 两点.
的终边分别与单位圆相交于A,B 两点.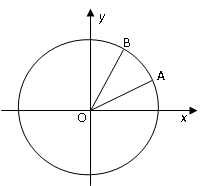
(Ⅰ)若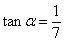 ,
, ,求
,求 的值;
的值;
(Ⅱ)若角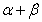 的终边与单位圆交于
的终边与单位圆交于 点,设角
点,设角 的正弦线分别为
的正弦线分别为 ,试问:以
,试问:以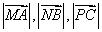 作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
(Ⅰ) (Ⅱ)以
(Ⅱ)以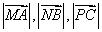 作为三边的长能构成一个三角形.
作为三边的长能构成一个三角形.
解析试题分析:(Ⅰ)∵0<α<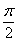 , tanα=
, tanα= ,∴cosα=
,∴cosα=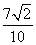 ,sinα=
,sinα=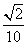 .
.
又∵0<β<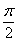 ,sinβ=
,sinβ=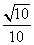 ,∴0<2β<π,cos2β=1-2sin2β=
,∴0<2β<π,cos2β=1-2sin2β=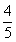 ,sin2β=
,sin2β=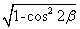 =
=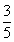 .
.
于是cos(α+2β)=cosαcos2β-sinαsin2β=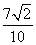 ×
×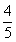 -
-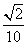 ×
×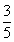 =
=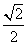 .
.
由已知条件知0<α+2β<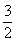 π,∴α+2β=
π,∴α+2β= . 6分
. 6分
(Ⅱ)解:以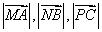 作为三边的长能构成一个三角形,证明如下:
作为三边的长能构成一个三角形,证明如下:
∵ ,∴
,∴
∴ ,
, ,
,
∵ ,所以
,所以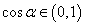 ,
, ,于是有:
,于是有: ① 8分
① 8分
又∵ ,∴
,∴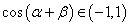 ,于是有:
,于是有: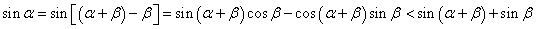 ②
②
同理: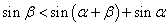 ③
③
由①②③可知,以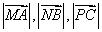 作为三边的长能构成一个三角形. 12分
作为三边的长能构成一个三角形. 12分
考点:同角间的三角函数关系及两角和的余弦公式
点评:第一问涉及到基本公式有

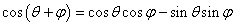 ,求角的大小常首先求角的某一三角函数值,结合角的范围即可求出;第二问判定能否构成三角形即判定三边长是否有任意两边之和大于第三边,确定不等式关系主要借助于正余弦函数的有解性
,求角的大小常首先求角的某一三角函数值,结合角的范围即可求出;第二问判定能否构成三角形即判定三边长是否有任意两边之和大于第三边,确定不等式关系主要借助于正余弦函数的有解性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的内角A、B、C所对的边为
的内角A、B、C所对的边为 ,
, 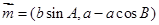 ,
,  ,且
,且 与
与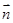 所成角为
所成角为 .
.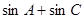 的取值范围.
的取值范围.
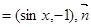
 ,
,
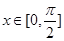 时,求函数
时,求函数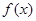 的值域:
的值域: 中,
中,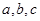 分别为角
分别为角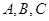 的对边,若
的对边,若 ,求边
,求边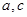 .
. ------①
------① ------②
------②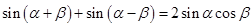 ------③
------③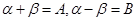 有
有
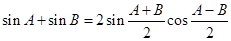 .
. ;
;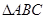 的三个内角
的三个内角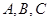 满足
满足 ,试判断
,试判断 <α<
<α<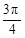 ,0<β<
,0<β< ,
,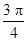 +β)=
+β)=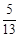 ,求sin(α+β)的值.
,求sin(α+β)的值. 为第二象限的角,
为第二象限的角, 为第三象限的角,
为第三象限的角, 。
。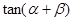 的值;
的值; 的值。
的值。 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角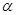 ,
, ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 两点,已知点
两点,已知点 的横坐标为
的横坐标为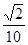 ,点
,点 的纵坐标为
的纵坐标为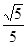 .
. 的值;
的值; 的值.
的值. ),
),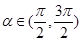
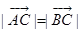 ,求角
,求角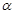 的值
的值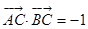 ,求
,求 的值
的值
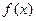 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;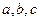 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若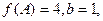 △ABC的面积为
△ABC的面积为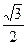 ,求
,求 的值
的值