题目内容
9.设函数f(x)=$\left\{\begin{array}{l}{(x+1)^{2},x<1}\\{4-\sqrt{x-1},x≥1}\end{array}\right.$,求使得f(a)=1的自变量a的取值.分析 根据已知中函数f(x)=$\left\{\begin{array}{l}{(x+1)^{2},x<1}\\{4-\sqrt{x-1},x≥1}\end{array}\right.$,分当a<1时和当a≥1时,两种情况讨论满足条件的a值,综合讨论结果可得答案.
解答 解:当a<1时,解f(a)=(a+1)2=1得:a=-2,或a=0,
当a≥1时,解f(a)=4-$\sqrt{a-1}$=1得:a=10,
综上所述:a=-2,或a=0,或a=10.
点评 本题考查的知识点是分段函数的应用,已知函数值求自变量,就是解方程.

练习册系列答案
相关题目
19.设集合A={1,3},集合B={1,2,5},则集合A∪B=( )
| A. | {1,2,5} | B. | {1} | C. | {1,2,3,5} | D. | {2,3,5} |
20.若sinα>0,则( )
| A. | cos2α>0 | B. | tan2α>0 | C. | $cos\frac{α}{2}>0$ | D. | $tan\frac{α}{2}>0$ |
17.已知函数f(x)=cos4x-sin4x,下列结论错误的是( )
| A. | f(x)=cos2x | B. | 函数f(x)的图象关于直线x=0对称 | ||
| C. | f(x)的最小正周期为π | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
19.若与球外切的圆台的上、下底面半径分别为r,R,则球的表面积为( )
| A. | 4π(r+R)2 | B. | 4πr2R2 | C. | 4πRr | D. | π(R+r)2 |
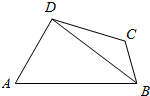 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.