题目内容
17.设A,B为椭圆$\frac{{x}^{2}}{4}$+y2=1上满足OA⊥OB(O为原点)的两点.(1)以O为极点,Ox轴为极轴建立极坐标系,求椭圆的极坐标方程;
(2)求$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$的值;
(3)判断直线AB与圆C:x2+y2=$\frac{4}{5}$的位置关系.
分析 (1)直接把x=ρcosθ,y=ρsinθ代入椭圆$\frac{{x}^{2}}{4}$+y2=1求得椭圆的极坐标方程;
(2)对OB所在直线斜率存在和不存在分类讨论,通过联立直线方程和椭圆方程求得|OA|2、|OB|2,代入$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$求得答案;
(3)结合(2)中的结论,由三角形面积相等求得O到直线AB距离,再结合圆C的半径得到结论.
解答 解:(1)把x=ρcosθ,y=ρsinθ代入椭圆$\frac{{x}^{2}}{4}$+y2=1,得ρ2(cos2θ+4sin2θ)=4;
(2)当OA斜率为0时,OB斜率不存在,此时$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=\frac{1}{4}+1=\frac{5}{4}$.
当OB斜率存在时,设OB所在直线方程为y=kx,则OA所在直线方程为y=-$\frac{1}{k}x$.
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得:${x}^{2}=\frac{4}{1+4{k}^{2}}$,${y}^{2}=\frac{4{k}^{2}}{1+4{k}^{2}}$.
∴$|OB{|}^{2}=\frac{4(1+{k}^{2})}{1+4{k}^{2}}$.
联立$\left\{\begin{array}{l}{y=-\frac{1}{k}x}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得${x}^{2}=\frac{4{k}^{2}}{{k}^{2}+4}$,${y}^{2}=\frac{4}{{k}^{2}+4}$.
∴$|OA{|}^{2}=\frac{4(1+{k}^{2})}{{k}^{2}+4}$.
则$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{1+4{k}^{2}}{4(1+{k}^{2})}+\frac{{k}^{2}+4}{4(1+{k}^{2})}=\frac{5}{4}$.
综上$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{5}{4}$;
(3)由$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{5}{4}$,得4(|OA|2+|OB|2)=5|OA|2|OB|2,
∴4|AB|2=5(|OA|•|OB|)2,即$\frac{|OA|•|OB|}{|AB|}=\frac{2\sqrt{5}}{5}$.
也就是直角三角形AOB的直角顶点O到AB的距离为$\frac{2\sqrt{5}}{5}$.
而圆C:x2+y2=$\frac{4}{5}$的半径为$\frac{2\sqrt{5}}{5}$,
∴直线AB与圆C:x2+y2=$\frac{4}{5}$相切.
点评 本题考查椭圆的简单性质,考查了直线和椭圆的位置关系,体现了分类讨论的数学思想方法,(3)的判断具有一定的灵活性,属中高档题.

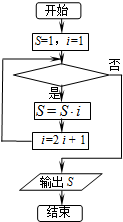
| A. | i≤31? | B. | i≤63? | C. | i≥63? | D. | i≤127? |
 有下列四个结论,
有下列四个结论, 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示,则该小区居民用电量的中位数为155,平均数为156.8.
某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示,则该小区居民用电量的中位数为155,平均数为156.8.