题目内容
【题目】已知极坐标系的极点与直角坐标系的原点重合，极轴与x轴的非负半轴重合．曲线 
（t为参数），曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ． （Ⅰ）将曲线C1 ， C2分别化为普通方程、直角坐标方程，并说明表示什么曲线；
（Ⅱ）设F（1，0），曲线C1与曲线C2相交于不同的两点A，B，求|AF|+|BF|的值．
【答案】解：（Ⅰ）曲线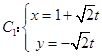 
（t为参数），
将曲线C1的参数方程消去参数t，
化为普通方程得y=﹣x+1，表示一条直线．
曲线C2的极坐标方程为ρ=ρcos2θ+8cosθ．
由cos2θ=1﹣2sin2θ，得曲线C2的方程可变形为ρ2sin2θ=4ρcosθ，
化为直角坐标方程可得y2=4x，曲线C2表示顶点在原点，焦点为（1，0）的抛物线
（Ⅱ）由 
，消去y，可得x2﹣6x+1=0
设A（x1，y1），B（x2，y2），则x1+x2=6，
由题意知F（1，0）为曲线C2的焦点
所以|AF|+|BF|=（x1+1）+（x2+1）=x1+x2+2=8
【解析】（Ⅰ）曲线C1的参数方程消去参数t，化为普通方程得y=﹣x+1，表示一条直线；由cos2θ=1﹣2sin2θ，得曲线C2的方程可变形为ρ2sin2θ=4ρcosθ，化为直角坐标方程可得y2=4x，曲线C2表示顶点在原点，焦点为（1，0）的抛物线．（Ⅱ）由 
，得x2﹣6x+1=0，由题意知F（1，0）为曲线C2的焦点，由此能求出|AF|+|BF|的值．
【题目】为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：
收入x（万元） | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y（万元） | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程 
，其中 
， 
= 
﹣ 
，据此估计，该社区一户居民年收入为15万元家庭的年支出为万元．
