��Ŀ����
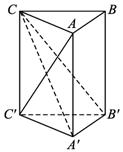
��ͼ�٣���ֱ������ABC-A1B1C1�У�BA=BC=2����ABC=90�㣬����ֱ��A1B��AC��60��Ľǣ���O��E�ֱ�����AC��BB1���е㣬��F����B1C1�ϵĶ��㣮����������ֱ��A1E��OF���ǵĴ�С��
����������B1-A1C-C1�Ĵ�С��
������O1ΪA1C1���е㣬��ͼ�ڣ�����ֱ������ABC-A1B1C1��ֱ��O1O��תһ�ܣ��߶�BC1��ת������ͼ�����ñض���
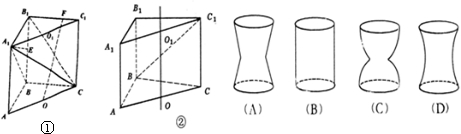
��������I����BΪ����ԭ�㣬��BA��BC��BB1����ֱ�߷ֱ�Ϊx��y��z�Ὠ���ռ�ֱ������ϵ��д��Ҫ�õĵ�����꣬������ĸߣ���������ֱ��A1B��AC��60��Ľǣ�д����������ֱ�ߵļнǣ�����ߣ����������ֱ�����ɵĽǣ�
��II�����ݽ���������ϵ������ƽ���һ���������������һ��ƽ��ķ����������ݷ�������ƽ���ϵ���������������0�����һ�����������������������ļн���������ǵ�ֵ��
��III������ֱ����������Ϊ������ABCD-A1B1C1D1����ͼ2������ת�����У��߶�BC1����һ�㵽��OO1�ľ��뱣�ֲ��䣬��BC1���е�ΪM��OO1���е�ΪO2����O2M������ֱ��OO1��BC1�Ĺ����߶Σ������ռ�ֱ������ϵ����ʧһ���ԣ����N���߶�MC1�ϣ�����������߳�Ϊ2��MN=t��PN=d���������
��II�����ݽ���������ϵ������ƽ���һ���������������һ��ƽ��ķ����������ݷ�������ƽ���ϵ���������������0�����һ�����������������������ļн���������ǵ�ֵ��
��III������ֱ����������Ϊ������ABCD-A1B1C1D1����ͼ2������ת�����У��߶�BC1����һ�㵽��OO1�ľ��뱣�ֲ��䣬��BC1���е�ΪM��OO1���е�ΪO2����O2M������ֱ��OO1��BC1�Ĺ����߶Σ������ռ�ֱ������ϵ����ʧһ���ԣ����N���߶�MC1�ϣ�����������߳�Ϊ2��MN=t��PN=d���������
����⣺��ͼ1����BΪ����ԭ�㣬��BA��BC��BB1����ֱ�߷ֱ�Ϊx��y��z�Ὠ���ռ�ֱ������ϵ����A��2��0��0����C��0��2��0����0��1��1��0��
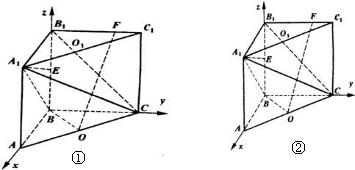
���������ĸ�Ϊh����A1��2��0��h����C��0��2��0����
=(2��-2��0)��
��cos��?
��
��=
��
��cos60��=
�����h=2��
��E��0��0��1����A1��202����
=(-2��0��-1)��
��FΪ��B1C1�ϵĶ��㣬�ʿ���f��0��y��2����
��
=(-1��y-1��2)��
��
•
=(-2��0��-1)•(-1��y-1��2)=0
��
��
��������ֱ��A1E��OF�ɽ�Ϊ90��
������֪ƽ��A1CC1��һ��������Ϊ
=��1��1��0������ƽ��A1B1C��һ��������Ϊ
=��x��y��1������
=(x��y��1)
•
=��x��y��1��•��-2��2��-2��=-2x+2y-2=0������
•
=��x��y��1��•��-2��0��0��=-2x=0������
�ɢ١��ڣ���
=(0��1��1��)��
��cos��
��
��=
=
=
��
�ࣼ
��
��=60�㣮
�������B1-A1C-C1�Ĵ�СΪ60�㣮
������ֱ����������Ϊ������ABCD-A1B1C1D1����ͼ2������ת�����У��߶�BC1����һ�㵽��OO1�ľ��뱣�ֲ��䣬
��BC1���е�ΪM��OO1���е�ΪO2����O2M������ֱ��OO1��BC1�Ĺ����߶Σ�
��N���߶�BC1������һ�㣬N����OO1�ϵ���ӰΪP��
�������������O2�����㽨���ռ�ֱ������ϵ����ʧһ���ԣ����N���߶�MC1�ϣ�����������߳�Ϊ2��MN=t��PN=d��
�ߣ�
��
��=45�㣬
��N(-
t��1��
t)��P(O��O��
t)��
��Rt��OPN����O2P2+PN2=O2N2����
d2+
t2=
t2+1+
t2����d2-
=1��
��d��t֮������˫���߹�ϵ����ѡD��

���������ĸ�Ϊh����A1��2��0��h����C��0��2��0����
| CA |
��cos��?
| BA1 |
| CA |
| ||||
|
|
��cos60��=
| 4 | ||||
2
|
��E��0��0��1����A1��202����
| A1E |
��FΪ��B1C1�ϵĶ��㣬�ʿ���f��0��y��2����
��
| OF |
��
| A1E |
| OF |
��
| A1E |
| OF |
������֪ƽ��A1CC1��һ��������Ϊ
| BO |
| n |
| n |
| n |
| A1C |
| n |
| A1C |
�ɢ١��ڣ���
| n |
��cos��
| n |
| BO |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
�ࣼ
| n |
| BO |
�������B1-A1C-C1�Ĵ�СΪ60�㣮
������ֱ����������Ϊ������ABCD-A1B1C1D1����ͼ2������ת�����У��߶�BC1����һ�㵽��OO1�ľ��뱣�ֲ��䣬
��BC1���е�ΪM��OO1���е�ΪO2����O2M������ֱ��OO1��BC1�Ĺ����߶Σ�
��N���߶�BC1������һ�㣬N����OO1�ϵ���ӰΪP��
�������������O2�����㽨���ռ�ֱ������ϵ����ʧһ���ԣ����N���߶�MC1�ϣ�����������߳�Ϊ2��MN=t��PN=d��
�ߣ�
| OO1 |
| BC1 |
��N(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
��Rt��OPN����O2P2+PN2=O2N2����
d2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| t2 |
| 2 |
��d��t֮������˫���߹�ϵ����ѡD��
���������⿼�����ÿռ���������������еļнǺ;�������⣬�������Ĺؼ��ǽ������ʵ�����ϵ�������Ժ�ǿ�������Ƶ�ת�������ֵ����㣬��������Ŀ���Ѷȣ�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ֱ֪������ABC-A1B1C1����ACB=90�㣬E����CC1�϶��㣬F��AB�е㣬AC=BC=2��AA1=4��
��ͼ����ֱ֪������ABC-A1B1C1����ACB=90�㣬E����CC1�϶��㣬F��AB�е㣬AC=BC=2��AA1=4��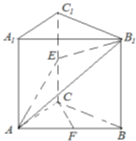 ��2013•μ�϶�ģ����ͼ����ֱ֪������ABC-A1B1C1�У���ACB=90�㣬E����CC1�ϵĶ��㣬F��AB���е㣬AC=BC=2��AA1=4��
��2013•μ�϶�ģ����ͼ����ֱ֪������ABC-A1B1C1�У���ACB=90�㣬E����CC1�ϵĶ��㣬F��AB���е㣬AC=BC=2��AA1=4�� ��ͼ����ֱ֪������ABC-A1B1C1�IJ��ⳤΪ2�������ABC�ǵ���ֱ�������Σ��ҡ�ACB=90�㣬AC=2��D��A A1���е㣮
��ͼ����ֱ֪������ABC-A1B1C1�IJ��ⳤΪ2�������ABC�ǵ���ֱ�������Σ��ҡ�ACB=90�㣬AC=2��D��A A1���е㣮