题目内容
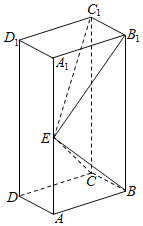
【题目】如图,长方体![]() 的底面
的底面![]() 是正方形,点
是正方形,点![]() 在棱
在棱![]() 上,
上,![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据长方体性质可知![]() 平面
平面![]() ,从而
,从而![]() ,由题意
,由题意![]() ,即可由线面垂直的判定定理证明
,即可由线面垂直的判定定理证明![]() 平面
平面![]() ;
;
(2)由题意![]() ,设
,设![]() ,建立空间直角坐标系,即可写出各个点的坐标,求得平面
,建立空间直角坐标系,即可写出各个点的坐标,求得平面![]() 和平面
和平面![]() 的法向量,即可由两个平面的法向量求得二面角
的法向量,即可由两个平面的法向量求得二面角![]() 夹角的余弦值,再由同角三角函数关系式即可求得二面角
夹角的余弦值,再由同角三角函数关系式即可求得二面角![]() 的正弦值.
的正弦值.
(1)由已知得,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() .
.
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由(1)知![]() .由题设知
.由题设知![]() ,所以
,所以![]() ,
,
故![]() ,
,![]() . 设
. 设![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 为单位长,建立如图所示的空间直角坐标系
为单位长,建立如图所示的空间直角坐标系![]() :
:
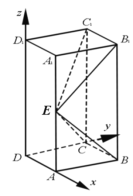
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则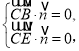 即
即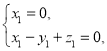 .
.
所以可取![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则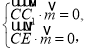 即
即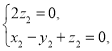
所以可取![]() .
.
于是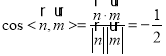 .
.
由同角三角函数关系式可得二面角![]() 的正弦值为
的正弦值为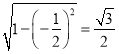 .
.

练习册系列答案
相关题目
【题目】某大学为了调查该校学生性别与身高的关系,对该校1000名学生按照![]() 的比例进行抽样调查,得到身高频数分布表如下:
的比例进行抽样调查,得到身高频数分布表如下:
男生身高频率分布表
男生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 (单位:厘米) |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
(1)估计这1000名学生中女生的人数;
(2)估计这1000名学生中身高在![]() 的概率;
的概率;
(3)在样本中,从身高在![]() 的女生中任取3名女生进行调查,设
的女生中任取3名女生进行调查,设![]() 表示所选3名学生中身高在
表示所选3名学生中身高在![]() 的人数,求
的人数,求![]() 的分布列和数学期望.(身高单位:厘米)
的分布列和数学期望.(身高单位:厘米)