题目内容
14.已知函数f(x)=cos2x+2$\sqrt{3}$sinxcosx-sin2x=$\sqrt{3}$sin2x+cos2x(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,A、B、C分别为三边a,b,c所对的角,若a=$\sqrt{3}$,f(a)=1,求b+c的最大值.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x+$\frac{π}{6}$),由周期公式可求函数f(x)的最小正周期,由-$\frac{π}{2}$+2kπ<2x+$\frac{π}{6}$<$\frac{π}{2}$+2kπ,k∈Z,解得函数f(x)的单调递增区间.
(2)由f(a)=1,可得2sin(2A+$\frac{π}{6}$)=1,结合0<A<π,可求A=$\frac{π}{3}$,由余弦定理可得3=(b+c)2-3bc,又bc≤($\frac{b+c}{2}$)2,可得3≥(b+c)2-3($\frac{b+c}{2}$)2,即可解得b+c的最大值.
解答 解:(1)∵f(x)=cos2x+2$\sqrt{3}$sinxcosx-sin2x=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$,
∴由-$\frac{π}{2}$+2kπ<2x+$\frac{π}{6}$<$\frac{π}{2}$+2kπ,k∈Z,解得函数f(x)的单调递增区间为:(-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ),k∈Z.
(2)由f(a)=1,可得2sin(2A+$\frac{π}{6}$)=1,又0<A<π,所以A=$\frac{π}{3}$.
由余弦定理可得a2=b2+c2-2bccosA,即3=b2+c2-bc=(b+c)2-3bc,
又bc≤($\frac{b+c}{2}$)2,
所以3=(b+c)2-3bc≥(b+c)2-3($\frac{b+c}{2}$)2,
故b+c$≤2\sqrt{3}$,当且仅当b=c且b2+c2-bc=3,即b=c=$\sqrt{3}$时等号成立.
因此b+c的最大值为2$\sqrt{3}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质,三角函数周期公式的应用,考查了余弦定理,基本不等式的应用,熟练掌握公式及定理是解题的关键,属于中档题.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案| A. | [-3,3] | B. | {-3,3} | C. | (-3,3) | D. | (-∞,-3]∪[3,+∞) |
| A. | $\frac{b}{c}$ | B. | $\frac{sinB}{sinA}$ | C. | $\frac{sinC}{c}$ | D. | $\frac{c}{sinC}$ |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{5}{10}$ | D. | $\frac{7}{10}$ |
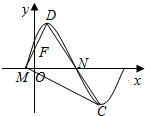 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.