题目内容
已知向量
,
,
满足
+
+
=
,|
|=2
,
与
-
所成的角为120°,则当t∈R时,|t
+(1-t)
|的取值范围是
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| c |
| 3 |
| c |
| a |
| b |
| a |
| b |
[
,+∞)
| 3 |
| 2 |
[
,+∞)
.| 3 |
| 2 |
分析:由向量的运算法则作出图象,并可知图中的数量关系,把问题转换为|
|的值,进而结合图象转化为:A到直线BD上动点的距离的取值范围,结合三角形的知识可得答案.
| AF |
解答: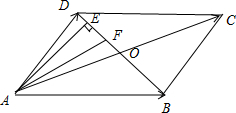 解:如图所示,
解:如图所示,
记向量
=
,
=
,-
=
,则
=
-
由题意结合向量的加减运算可得AC=2
,∠AOB=120°
在结合数乘的意义可得:|t
+(1-t)
|=|t(
-
)+
|=|t
+
|=|
+
|=|
|,
代表点A到直线BD上动点的距离,
而当t变化时,点F在直线BD上运动,当F运动到图中的点E处,
此时AE⊥BD,使点A到直线BD上动点的距离最小,
在RT△AOE中,AO=
,AE=AOsin∠AOB=
,故|t
+(1-t)
|≥AE=
,
故答案为:[
,+∞)
 解:如图所示,
解:如图所示,记向量
| AB |
| a |
| AC |
| b |
| AC |
| c |
| DB |
| a |
| b |
由题意结合向量的加减运算可得AC=2
| 3 |
在结合数乘的意义可得:|t
| a |
| b |
| a |
| b |
| b |
| DB |
| AD |
| DF |
| AD |
| AF |
代表点A到直线BD上动点的距离,
而当t变化时,点F在直线BD上运动,当F运动到图中的点E处,
此时AE⊥BD,使点A到直线BD上动点的距离最小,
在RT△AOE中,AO=
| 3 |
| 3 |
| 2 |
| a |
| b |
| 3 |
| 2 |
故答案为:[
| 3 |
| 2 |
点评:本题为向量最值得求解,数形结合把问题转化为点A到直线BD上动点的距离是解决问题的关键,属中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π. sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π. sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π.