题目内容
已知a∈R,函数f(x)=2x3-3(a+1)x2+6ax.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若a=2,求f(x)在闭区间[0,4]上的最小值.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若a=2,求f(x)在闭区间[0,4]上的最小值.
(1)当a=1时,f(x)=2x3-6x2+6x,
导数f'(x)=6x2-12x+6,
所以f'(2)=6×22-12×2+6=6,
又因为f(2)=2×23-6×22+6×2=4,
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-4=6(x-2),即6x-y-8=0.
(2)当a=2时,f(x)=2x3-9x2+12x,
导数f'(x)=6x2-18x+12=6(x-1)(x-2).
令f'(x)=0,得x1=1,x2=2.
比较f(0)、f(1)、f(2)、f(4)的大小可知f(0)最小,
故函数f(x)在闭区间[0,4]上的最小值是0.
导数f'(x)=6x2-12x+6,
所以f'(2)=6×22-12×2+6=6,
又因为f(2)=2×23-6×22+6×2=4,
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-4=6(x-2),即6x-y-8=0.
(2)当a=2时,f(x)=2x3-9x2+12x,
导数f'(x)=6x2-18x+12=6(x-1)(x-2).
令f'(x)=0,得x1=1,x2=2.
| x | 0 | (0,1) | 1 | (1,2) | 2 | (2,4) | 4 |
| f'(x) | 12 | + | 0 | - | 0 | + | 36 |
| f(x) | 0 | 单调递增 | 极大值5 | 单调递减 | 极小值4 | 单调递增 | 32 |
故函数f(x)在闭区间[0,4]上的最小值是0.

练习册系列答案
相关题目
 则
则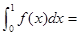 ( )
( )