题目内容
【题目】已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
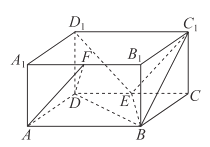
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点为
中点为![]() ,求证四边形
,求证四边形![]() 为平行四边形,即可由线线平行推证线面平行;
为平行四边形,即可由线线平行推证线面平行;
(2)以![]() 为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
为坐标原点,建立空间直角坐标系,通过求解两平面法向量之间夹角的余弦值,从而求得二面角夹角的余弦值.
(1)证明:∵![]() ,
,![]() ,∴
,∴![]() 是
是![]() 中点,
中点,
取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,如下图所示:
,如下图所示:
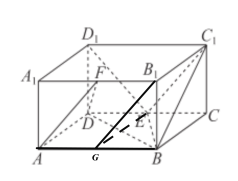
则在菱形![]() 中,
中,![]() ,
,![]() //
//![]()
∵![]() ,
,![]() //
//![]() ,∴
,∴![]() ,
,![]() //
//![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() //
//![]() ,
,
又![]() ,
,![]() //
//![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() //
//![]() ,∴
,∴![]() //
//![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]() .即证.
.即证.
(2)以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 建立如图所示的空间的直角坐标系.
建立如图所示的空间的直角坐标系.
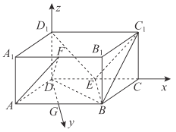
因为已知该四棱柱为直四棱柱,![]() ,
,![]() ,
,
所以![]() 为等边三角形.
为等边三角形.
因为![]() ,所以点
,所以点![]() 是
是![]() 的中点.
的中点.
故点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
由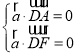 得
得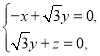
取![]() ,得
,得![]() ,
,![]() ,
,
故![]()
![]() .
.
∵![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
∴![]() ,∴
,∴![]() 是平面
是平面![]() 的法向量,
的法向量,
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,
,
则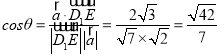 .
.
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】高考的成绩不仅需要平时的积累,还与考试时的状态有关系.为了了解考前学生的紧张程度与性别是否有关系,现随机抽取某校500名学生进行了调查,结果如表所示:
心情 性别 | 男 | 女 | 总计 |
正常 | 30 | 40 | 70 |
焦虑 | 270 | 160 | 430 |
总计 | 300 | 200 | 500 |
(1)根据该校调查数据,能否在犯错误的概率不超过0.01的前提下,认为“该学校学生的考前焦虑情况与性别有关”?
(2)若从考前心情正常的学生中按性别用分层抽样的方法抽取7人,再从被抽取的7人中随机抽取2人,求这两人中有女生的概率.
附: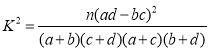 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |