题目内容
△ABC中,A=60°,b=4
,为使此三角形只有一个,则a应满足的条件为( )
| 3 |
A.0<a<4
| B.a=6 | ||||
C.a≥4
| D.0<a≤4
|
∵△ABC中,A=60°,b=4
,
∴作出△ABC的示意图,如图所示
可得点C到直线AB的最短距离为4
sin60°=6
以C为圆心,CB长为半径画弧,
则当圆弧与射线AB有且只有一个公共点时,满足条件的△ABC只有一个,
∵当圆弧半径R=6时,圆弧与射线AB相切,有唯一公共点;
当圆弧半径R≥4
时,圆弧与直线AB相交有两个交点,但只有一个交点在射线AB上
∴当BC=6或BC≥4
时,满足条件的△ABC只有一个,即a≥4
或a=6
故选:C

| 3 |
∴作出△ABC的示意图,如图所示
可得点C到直线AB的最短距离为4
| 3 |
以C为圆心,CB长为半径画弧,
则当圆弧与射线AB有且只有一个公共点时,满足条件的△ABC只有一个,
∵当圆弧半径R=6时,圆弧与射线AB相切,有唯一公共点;
当圆弧半径R≥4
| 3 |
∴当BC=6或BC≥4
| 3 |
| 3 |
故选:C


练习册系列答案
相关题目

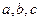 为
为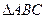 的三个内角
的三个内角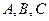 的对边,向量
的对边,向量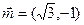 ,
,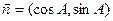 ,若
,若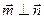 ,且
,且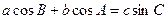 ,则角
,则角