题目内容

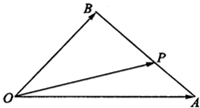如图，在△OAB中，已知P为线段AB上的一点，若
BP
=3
PA
，|
OA
|=4，|
OB
|=2，且
OA
与
OB
的夹角为60°，则
OP
•
AB
=
-9
-9
．
分析：用
OA
和
OB
当基底，表示
OP
和
AB
，则要求的式子变为（
3
4
OA
+
1
4
OB
 ）•（
OB
-
OA
），再利用两个向量的数量积的定义，数量积公式运算求得结果．
解答：解：由题意可得
OP
=
OB
+
BP 
=
OB
+
3
4
BA
=
OB
+
3
4
（
OA
-
OB
）=
3
4
OA
+
1
4
OB
．
AB
=
OB
-
OA
．
∴
OP
•
AB
=（
3
4
OA
+
1
4
OB
 ）•（
OB
-
OA
）=
1
2
OA
•
OB
-
3
4
OA
2+
1
4
OB
2=
1
2
×4×2cos60°-
3
4
×16+
1
4
×4=-9．
故答案为-9．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义，数量积公式的应用，属于中档题．
练习册系列答案
相关题目
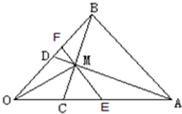精英家教网如图，在△OAB中，
OC
=
1
3
OA
，
OD
=
1
2
OB
，AD与BC交于点M，
设
OA
=
a
，
OB
=
b
，
（1）试用向量
a
和
b
表示
OM
；
（2）在线段AC上取一点E，线段BD上取一点F，使EF过M点，
OE
=λ
OA
，
OF
=μ
OB
，求证：
1
λ
+
2
μ
=5．
（2013•杭州二模）如图，在△OAB中，C为OA上的一点，且
OC
=
2
3
OA
，D是BC的中点，过点A的直线l∥OD，P是直线l上的任意点，若
OP
=λ1
OB
+λ2
OC
，则λ1-λ2=
-
3
2
-
3
2
．
如图，在△OAB中，已知|O
A
| =2，|O
B
| =2
3
，∠AOB=90°，单位圆O与OA交于C，A
D
=λ
B
，λ∈(0，1)，P为单位圆O上的动点．
（1）若O
C
+O
P
=O
D
，求λ的值；
（2）记|P
D
|的最小值为f（λ），求f（λ）的表达式及f（λ）的最小值．
如图，在△OAB中，延长BA到C，使AC=BA，在OB上取点D，使DB=
1
3
OB，DC与OA交于E，设
OA
=
a
，
OB
=
b
，用
a
，
b
表示向量
OC
，
DC
，
DE
．
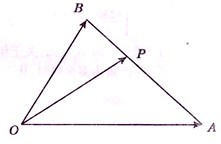如图，在△OAB中，已知P为线段AB上的一点，且|
AP
|=2|
PB
|．
（Ⅰ）试用
OA
，
OB
表示
OP
；
（Ⅱ）若|
OA
|=3，
|OB|
=2，且∠AOB=60°，求
OP
•
AB
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网