题目内容
(本题满分14分,第1小题6分,第2小题8分)
已知函数 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
已知函数
 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若
 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.(1) ,
, 。(2)直角三角形.
。(2)直角三角形.
 ,
, 。(2)直角三角形.
。(2)直角三角形.试题分析:(1)


 ……………………3分
……………………3分因为
 所以
所以 ,…………………………………………………………4分
,…………………………………………………………4分令–
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ得到:单调增区间为
+2kπ得到:单调增区间为 (k∈Z)………6分
(k∈Z)………6分( 无(k∈Z)扣1分 )
(2) 因为
 ,则
,则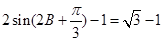 ,所以
,所以 ………………8分
………………8分又
 ,则
,则 ,
,
化简得
 ,所以
,所以 ,…………………………………………………12分
,…………………………………………………12分所以
 ,故△ABC为直角三角形.…………………………………………………14分
,故△ABC为直角三角形.…………………………………………………14分 的单调性和最值;正弦定理。
的单调性和最值;正弦定理。点评:求三角函数的最值、周期、单调区间等,一般要把三角函数化为
 的形式。但在求单调区间时,一定要注意
的形式。但在求单调区间时,一定要注意 的正负。
的正负。
练习册系列答案
相关题目
 =(
=( ,1),
,1), =(
=( ,
,  )且
)且 .
. 的取值范围.
的取值范围. ,则外接圆的半径为___
,则外接圆的半径为___ 中,
中, .
. 的大小;
的大小; ,
, ,求
,求 .
. .
. ,求a,b;
,求a,b;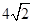 n mile内有暗礁,海轮由西向东航行,望见这岛在北偏东60°,航行6 n mile以后,望见这岛在北偏东30°. 如果这艘海轮不改变航向继续前行,则经过________n mile后海轮会触礁.
n mile内有暗礁,海轮由西向东航行,望见这岛在北偏东60°,航行6 n mile以后,望见这岛在北偏东30°. 如果这艘海轮不改变航向继续前行,则经过________n mile后海轮会触礁.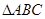 中,角
中,角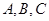 所对的边分别为
所对的边分别为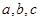 ,且满足
,且满足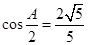 ,
,
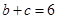 ,求
,求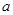 的值.
的值. 中,
中, 。求
。求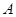 是
是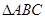 的一个内角,若
的一个内角,若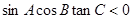 ,则
,则