题目内容
1．将正整数从1开始依次写下来，直至2015为止，得到一个新的正整数：1234…201320142015．这个正整数是几位数（ ）| A． | 3506位数 | B． | 4518位数 | C． | 6953位数 | D． | 7045位数 |
分析 由于从1到2015共有9个一位数，90个两位数，900个三位数，1016个四位数，相加可得1234…201320142015的位数．
解答 解：将正整数从1开始依次写下来，直至2015为止，得到一个新的正整数：1234…201320142015．
由于从1到2015共有9个一位数，90个两位数，900个三位数，1016个四位数，
故1234…201320142015的位数为：9+90×2+900×3+1016×4=6953，
故选：C
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
阅读快车系列答案
相关题目
9．七个同学参加三个兴趣小组，每人只能参加一个兴趣小组，每个兴趣小组至少两个同学，则不同的参加方法有（ ）
| A． | 630种 | B． | 210种 | C． | 420种 | D． | 1890种 |
16．下面几种推理中是类比推理的是（ ）
| A． | n边形内角和为f（n）=（n-2）π，则5边形内角和为f（5）=（5-2）π=3π | |
| B． | 某班张三、李四、王五身高都超过1.8米，猜想该班同学身高都超过1.8米 | |
| C． | 猜想数列1×2，2×3，3×4，…的通项公式为an=n（n+1）（n∈N+） | |
| D． | 由平面直角坐标系中两点P1（x，y），P2（a，b）之间距离为d=$\sqrt{（x-a）^{2}+（y-b）^{2}}$，推测空间直角坐标系中两点P1（x，y，z），P2（a，b，c）之间距离为d=$\sqrt{（x-a）^{2}+（y-b）^{2}+（z-c）^{2}}$ |
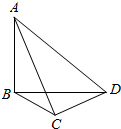若电视塔AB的高度为30米，且在D，C两点的仰视角分别为45度和60度，且∠DBC=30°，则C，D两点间的距离是多少米．