题目内容
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
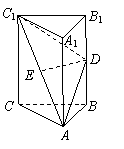 (Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小。
(Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小。
解法一:(Ⅰ)设O为AC中点,连接EO,BO,则EO∥=C1C,又C1C∥=B1B,所以EO∥=DB,EOBD为平行四边形,ED∥OB. ……2分
∵AB=BC,∴BO⊥AC,
 又平面ABC⊥平面ACC1A1,BOÌ面ABC,故BO⊥平面ACC1A1,
又平面ABC⊥平面ACC1A1,BOÌ面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.……6分
(Ⅱ)连接A1E,由AA1=AC=AB可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面ACC1A1和EDÌ平面ADC1知平面
ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A1F,则A1F⊥AD,∠A1FE为二面角A1-AD-C1的平面角.
不妨设AA1=2,则AC=2,AB=ED=OB=1,EF==,
tan∠A1FE=,∴∠A1FE=60°.
所以二面角A1-AD-C1为60°. ………12分
解法二:
(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点.
设A(a,0,0),B(0,b,0),B1(0,b,2c).
则C(-a,0,0),C1(-a,0,2c),E(0,0,c),D(0,b,c). ……3分
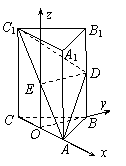 =(0,b,0),=(0,0,2c).
=(0,b,0),=(0,0,2c).
·=0,∴ED⊥BB1.
又=(-2a,0,2c),
·=0,∴ED⊥AC1, ……6分
所以ED是异面直线BB1与AC1的公垂线.
(Ⅱ)不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2),
=(-1,-1,0),=(-1,1,0),=(0,0,2),
·=0,·=0,即BC⊥AB,BC⊥AA1,又AB∩AA1=A,
∴BC⊥平面A1AD.
又 E(0,0,1),D(0,1,1),C(-1,0,1),
=(-1,0,-1),=(-1,0,1),=(0,1,0),
·=0,·=0,即EC⊥AE,EC⊥ED,又AE∩ED=E,
∴ EC⊥面C1AD. ……10分
cos<,>==,即得和的夹角为60°.
所以二面角A1-AD-C1为60°.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案



