题目内容
【题目】正方体ABCD﹣A1B1C1D1的棱和六个面的对角线共24条,其中与体对角线AC1垂直的有条.
【答案】6
【解析】解:如图,连接AC,则BD⊥AC.
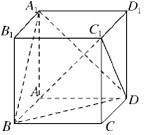
在正方体ABCD﹣AA1B1C1D1中,
∵C1C⊥平面BCD,
BD平面BCD,
∴C1C⊥BD,
又AC∩CC1=C,
∴BD⊥平面ACC1,
∵AC1平面ACC1,
∴AC1⊥BD.
同样A1B,A1D,B1D1,CD1,B1C都与AC1垂直.
正方体ABCD﹣A1B1C1D1的棱中没有与AC1垂直的棱,
故正方体ABCD﹣A1B1C1D1的棱和六个面的对角线共24条,其中与体对角线AC1垂直的有6条.
所以答案是:6.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |

(Ⅰ)在抽样的100人中,求对A餐厅评分低于30的人数;
(Ⅱ)从对B餐厅评分在[0,20)范围内的人中随机选出2人,求2人中恰有1人评分在[0,10)范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.

