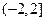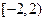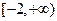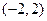题目内容
设集合P={1,2,3,4,5},对任意k∈P和正整数m,记f(m,k)=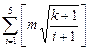 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
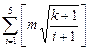 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。证明略
证明:定义集合A={
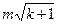 |m∈N*,k∈P},其中N*为正整数集。由于对任意k、i∈P且k≠i,
|m∈N*,k∈P},其中N*为正整数集。由于对任意k、i∈P且k≠i,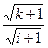 是无理数,则对任意的k1、k2∈P和正整数m1、m2,
是无理数,则对任意的k1、k2∈P和正整数m1、m2,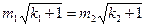 当且仅当m1=m2,k1=k2。由于A是一个无穷集,现将A中的元素按从小到大的顺序排成一个无穷数列。对于任意的正整数n,设此数列中第n项为
当且仅当m1=m2,k1=k2。由于A是一个无穷集,现将A中的元素按从小到大的顺序排成一个无穷数列。对于任意的正整数n,设此数列中第n项为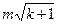 。下面确定n与m、k的关系。若
。下面确定n与m、k的关系。若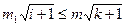 ,则
,则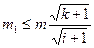 。由m1是正整数可知,对i=1,2,3,4,5,满足这个条件的m1的个数为
。由m1是正整数可知,对i=1,2,3,4,5,满足这个条件的m1的个数为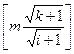 。从而n=
。从而n=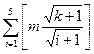 =f(m,k)。因此对任意n∈N*,存在m∈N*,k∈P,使得f(m,k)=n。
=f(m,k)。因此对任意n∈N*,存在m∈N*,k∈P,使得f(m,k)=n。
练习册系列答案
相关题目
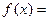
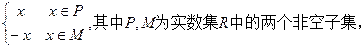 规定
规定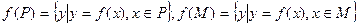 。给出四个判断
。给出四个判断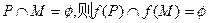
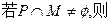
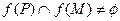
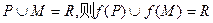
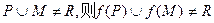
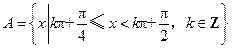 ,集合
,集合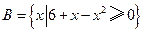 ,求
,求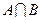 .
.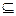 A,且A∩B={1,a}?若存在,求出实数a的值;若不存在,说明理由.
A,且A∩B={1,a}?若存在,求出实数a的值;若不存在,说明理由.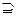 B且B≠
B且B≠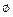 ,求实数m的取值范围。
,求实数m的取值范围。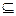 A,则实数m的取值范围为( )
A,则实数m的取值范围为( )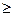 2
2 2
2 <0},B={x|x2+ax+b≤0},A∩B=
<0},B={x|x2+ax+b≤0},A∩B= ,
, .
.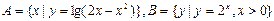 ,R是实数集,则
,R是实数集,则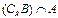 =( )
=( )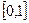
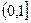
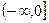
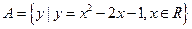 ,
,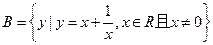 ,则
,则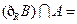 ()
()