题目内容
【题目】如图，椭圆
：
的离心率是
，过点
的动直线
与椭圆相交于
，
两点，当直线平行
轴时，直线被椭圆截得的线段长为4.
（1）求椭圆的方程；
（2）设
为坐标原点，是否存在常数
，使得
为定值？若存在，求的值；若不存在，请说明理由.
【答案】（1）
（2）存在；
【解析】
（1）由椭圆的离心率为
，过点
的动直线与椭圆相交于
，
两点，列出方程组求出，由此能求出椭圆的方程；
（2）当直线
的斜率存在时，设直线为
，与椭圆联立得，
，由此利用根的判别式，韦达定理，向量的数量积，结合已知条件推出
为定值，当直线的斜率不存在时，
,从而得到答案.
（1）解：由题设知
，
，
，
设椭圆方程为
，令
，得
，∴
，
解得
，所以椭圆
的方程为.
（2）当直线的斜率存在时，设直线的方程为，，的坐标分别为
，
，联立
得，
其判别式
，所以
，
.
从而
，
所以，当
，即时，.
此时，为定值.
当直线斜率不存在时，此时
，
，
∴.
故存在常数，使得
为定值
.
【题目】统计学中，经常用环比、同比来进行数据比较，环比是指本期统计数据与上期比较，如
年
月与年
月相比，同比是指本期数据与历史同时期比较，如年月与
年月相比.
环比增长率
（本期数
上期数）
上期数
，
同比增长率（本期数同期数）同期数.
下表是某地区近
个月来的消费者信心指数的统计数据：
序号 |
|
|
|
|
|
|
|
|
时间 |
|
|
|
|
|
|
|
|
消费者信心指数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
求该地区
年
月消费者信心指数的同比增长率（百分比形式下保留整数）；
除年
月以外，该地区消费者信心指数月环比增长率为负数的有几个月？
由以上数据可判断，序号
与该地区消费者信心指数
具有线性相关关系，写出关于的线性回归方程
（
，
保留
位小数），并依此预测该地区年月的消费者信心指数（结果保留位小数，参考数据与公式：
，
，
，
，
）
【题目】某种设备随着使用年限的增加，每年的维护费相应增加.现对一批该设备进行调查，得到这批设备自购入使用之日起，前5年平均每台设备每年的维护费用大致如表：
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知
.
（I）求表格中
的值；
（II）从这
年中随机抽取两年，求平均每台设备每年的维护费用至少有
年多于
万元的概率；
（Ⅲ）求
关于
的线性回归方程；并据此预测第几年开始平均每台设备每年的维护费用超过万元.
参考公式：用最小二乘法求线性回归方程
的系数公式：
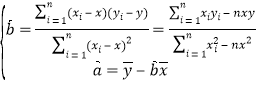
【题目】为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验.为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
（1）由以上统计数据填写下面
列联表，并判断能否在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”？
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附：
，其中
.
临界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中，记成绩不优良的乙班人数为
，求的分布列及数学期望.
