题目内容
设函数
.
（Ⅰ）求函数f (x)在点(0, f (0))处的切线方程；
（Ⅱ）求f (x)的极小值；
（Ⅲ）若对所有的
，都有
成立，求实数a的取值范围.
【答案】
(Ⅰ)∵f(x)的定义域为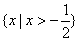
，又∵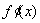
=2ln(2x+1)+2,
∴
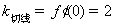，切点为O(0,0)，∴所求切线方程为y=2x. …………2分
(Ⅱ) 设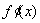=0，得ln(2x+1)=－1，得
；
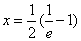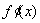>0，得ln(2x+1)>－1，得
；
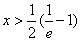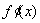<0，得ln(2x+1)<－1，得
；
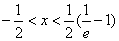则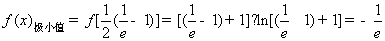
.…………6分
(Ⅲ)令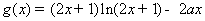
，
则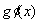
=2ln(2x+1)+ a=2[ln(2x+1)+1－a].
令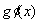=0，得ln(2x+1)= a－1，得
；
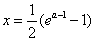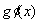>0，得ln(2x+1)> a－1，得
；
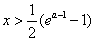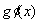<0，得ln(2x+1)< a－1，得
；
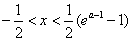（1）当a≤1时，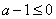
，∵
，
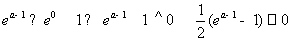∴对所有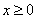
时，都有
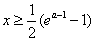，于是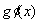≥0恒成立，
∴g(x)在[0,+∞)上是增函数.
又g(0)=0,于是对所有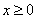,都有g(x)≥ g(0)=0成立.
故当a≤1时，对所有的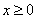，都有
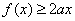成立.
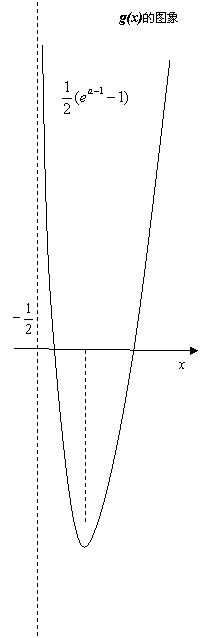
（2）当a>1时，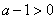
，∵
，
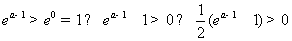∴对所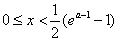有
，都有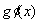<0恒成立，
∴g(x)在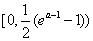
上是减函数.
又g(0)=0,于是对所有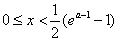,都有g(x)≤ g (0)=0.
故当a>1时，只有对仅有的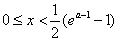，都有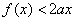
.
即当a>1时，不是对所有的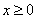，都有.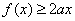
综合（1），（2）可知实数a的取值范围(－∞,1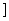
.……………………12分
练习册系列答案
相关题目
