题目内容
已数列 满足条件:
满足条件: (
( *)
*)
(Ⅰ)令 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)令 ,求数列
,求数列 的前n项和
的前n项和 。
。
解: (Ⅰ)由
(Ⅰ)由 得
得
 即
即
∴
∴数列 是等比数列;
是等比数列;
(Ⅱ) 由(Ⅰ)知数列
由(Ⅰ)知数列 是等比数列,
是等比数列, 公比为2,
公比为2,
∴
∵  ,
,
∴

 由此解得:
由此解得:
(Ⅲ)由( Ⅰ)得
Ⅰ)得  ,又
,又 ,
,
∴  ,
,


 (1)
(1) 得
得 (2)
(2)
(1)-(2)得 [来源:学+科+网]
[来源:学+科+网]
∴ 
∴
= 。
。
解析

练习册系列答案
相关题目
已知数列{an}满足an=n·pn(n∈N+,0< p<l),下面说法正确的是( )
①当p=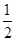 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当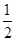 <p<l时,数列{an}不一定有最大项;
<p<l时,数列{an}不一定有最大项;
③当0<p<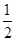 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项
| A.①② | B.③④ | C.②④ | D.②③ |
已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a1=1,那么a10=( )
| A.1 | B.9 | C.10 | D.55 |
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}的前n项和,则log2(S2012+2)等于( )
| A.2013 | B.2012 | C.2011 | D.2010 |
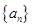 中,
中,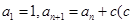 为常数,
为常数, ,且
,且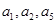 成公比不等于1的等比数列.
成公比不等于1的等比数列.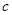 的值;
的值; ,求数列
,求数列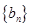 的前
的前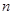 项和
项和 。
。 ,
,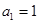 ,前
,前 项和为
项和为 .各项均为正数的等比数列列
.各项均为正数的等比数列列 满足:
满足: ,
, ,且
,且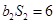 .
.
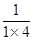 ,
,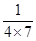 ,
,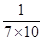 ,……,
,……, ,……
,……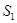 ,
,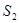 ,
,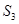 ,
,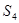
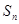 的表达式并用数学归纳法证明你的猜想。
的表达式并用数学归纳法证明你的猜想。 的前
的前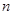 项和
项和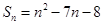 ,
,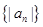 的前
的前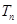 .
.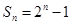 ,则
,则 = _________ .
= _________ .