题目内容
已知函数y=2sin(3x+
)
（1）利用五点法作出函数在x∈[-
，
]上的图象．
（2）当x∈R时，求f（x）的最小正周期；
（3）当x∈R时，求f（x）的单调递减区间；
（4）当x∈R时，求f（x）图象的对称轴方程，对称中心坐标．
| π |
| 2 |
（1）利用五点法作出函数在x∈[-
| π |
| 6 |
| π |
| 2 |
（2）当x∈R时，求f（x）的最小正周期；
（3）当x∈R时，求f（x）的单调递减区间；
（4）当x∈R时，求f（x）图象的对称轴方程，对称中心坐标．
分析：利用三角函数的图象研究函数的性质即可．
解答：解：（1）
（2）三角函数的周期T=
．
（3）由2kπ+
≤3x+
≤2kπ+
，得
≤3≤
+
，即函数的单调递减区间为[
，
+
](k∈Z)．
（4）由3x+
=
+kπ，解得x=
(k∈Z)，由3x+
=kπ，得x=
-
，即对称中心为（
-
，0）．
| x | -
|
0 |
|
|
| ||||||||
3x+
|
0 |
|
π |
|
2π | ||||||||
y=2sin(3x+
|
0 | 2 | 0 | -2 | 0 |
| 2π |
| 3 |
（3）由2kπ+
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 2kπ |
| 3 |
| 2kπ |
| 3 |
| π |
| 3 |
| 2kπ |
| 3 |
| π |
| 3 |
| 2kπ |
| 3 |
（4）由3x+
| π |
| 2 |
| π |
| 2 |
| kπ |
| 3 |
| π |
| 2 |
| kπ |
| 3 |
| π |
| 6 |
| kπ |
| 3 |
| π |
| 6 |
点评：本题主要考查三角函数的图象和性质，要求熟练掌握相应的三角函数的性质．
练习册系列答案
相关题目
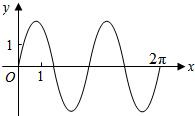已知函数y=2sin（ωx+φ）（ω＞0））在区间[0，2π]的图象如图：那么ω=（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin（wx+θ）为偶函数，其图象与直线y=2某两个交点的横坐标分别为x1，x2，若|x2-x1|的最小值为π，则该函数在区间（ ）上是增函数．
A、(-
| ||||
B、(-
| ||||
C、(0，
| ||||
D、(
|
下列4个命题：