题目内容
4.设10m=2,10n=3.则10-2m-10-n=-$\frac{1}{12}$.分析 利用指数的运算性质即可得出.
解答 解:∵10m=2,10n=3.
∴102m=4,$1{0}^{-n}=\frac{1}{3}$,
∴10-2m-10-n=$\frac{1}{4}$-$\frac{1}{3}$=-$\frac{1}{12}$.
故答案为:-$\frac{1}{12}$.
点评 本题考查了指数的运算性质,考查了计算能力,属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
14.数列{an},{bn}都是等比数列,当n≤3时,bn-an=2n,若数列{an}唯一,则a1=( )
| A. | -2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 1 |
15.不等式(x-y)(x+y)≥0所表示的平面区域为( )
| A. | 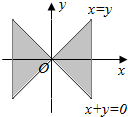 | B. | 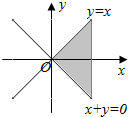 | C. | 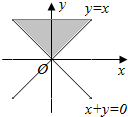 | D. | 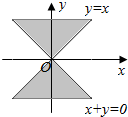 |