题目内容
设函数f(x)=lnx-px+1
(1)当P>0时，若对任意x>0，恒有f(x)≤0,求P的取值范围
（2）证明：
(n∈N
，n≥2)
（1）P≥1 （2）证明如下
解析:
（1）f(x)=ln2x-px+1定义域（0，+∞）,f′(x)=
-p=
=
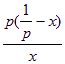
当P>0时，令f′(x)=0,x=
（0，+∞）
当x∈(0, 
)时，f′(x)>0 f(x)为增函数，
当x∈( ，+∞)时f′(x)<0
f(x)为减函数。
f(x)max=f()=ln
要使f(x)≤0恒成立只要f()=ln≤0
∴P≥1
（2）令P=1 由（1）知：lnx-x+1≤0
∴lnx≤x-1 n≥2
lnn2≤n2-1 
∴
=(n-1)-(
)
<(n-1)-[
]
=(n-1)-(
+
)
=(n-1)-(
)
=
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
,则函数f(
)+f(
)的定义域为_______.