题目内容
函数y= 的单调递减区间是 ( )
的单调递减区间是 ( )
 的单调递减区间是 ( )
的单调递减区间是 ( )| A.(-∞,-3) | B.(-1,+∞) | C.(-∞,-1 ) | D.[-1,+∞) |
A
分析:确定函数的定义域,求出二次函数的单调减区间,从而可得函数的单调区间.
解答:解:由x2+2x-3≥0,可得x≥1或x≤-3,∴函数的定义域为(-∞,-3]∪[1,+∞)
∵x2+2x-3=(x+1)2-4,
∴f(x)= x2+2x-3在(-∞,-1]上单调递减
∴函数y=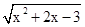
的单调递减区间是(-∞,-3]
故答案为:A
点评:本题考查函数的单调性,考查解不等式,属于基础题.
解答:解:由x2+2x-3≥0,可得x≥1或x≤-3,∴函数的定义域为(-∞,-3]∪[1,+∞)
∵x2+2x-3=(x+1)2-4,
∴f(x)= x2+2x-3在(-∞,-1]上单调递减
∴函数y=
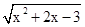
的单调递减区间是(-∞,-3]
故答案为:A
点评:本题考查函数的单调性,考查解不等式,属于基础题.

练习册系列答案
相关题目
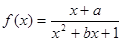 是奇函数,
是奇函数,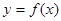 在
在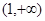 的单调性,并利用定义加以证明
的单调性,并利用定义加以证明 是奇函数.
是奇函数.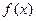 的单调性(不需要写出理由);
的单调性(不需要写出理由); ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.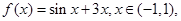 如果
如果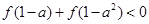 ,则实数
,则实数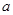 的取值范围是( )
的取值范围是( )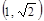
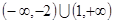
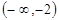
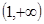
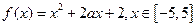
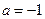 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;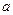 的取值范围,使
的取值范围,使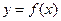 在区间
在区间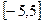 上是单调减函数
上是单调减函数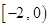 ∪
∪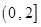 上的奇函数,当
上的奇函数,当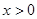 时,f(x)的图象如右图所示,那么f(x)的值域是
时,f(x)的图象如右图所示,那么f(x)的值域是 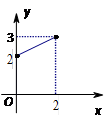
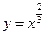 ,则其值域为 ▲
,则其值域为 ▲ 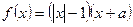 为奇函数,则
为奇函数,则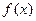 的增区间为_________________
的增区间为_________________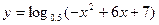 的单调递增区间为 。
的单调递增区间为 。