题目内容
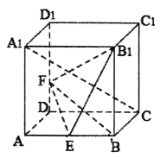
【题目】(理)在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上移动.
上移动.
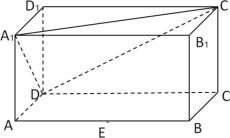
(1)探求![]() 多长时,直线
多长时,直线![]() 与平面
与平面![]() 成
成![]() 角;
角;
(2)点![]() 移动为棱
移动为棱![]() 中点时,求点
中点时,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)法一:先找出直线![]() 与平面
与平面![]() 所成角,再根据直角三角形解
所成角,再根据直角三角形解![]() ;法二:建立空间直角坐标系,先求平面法向量,再利用向量数量积求向量夹角,最后解方程得结果;
;法二:建立空间直角坐标系,先求平面法向量,再利用向量数量积求向量夹角,最后解方程得结果;
(2)建立空间直角坐标系,先求平面法向量,再利用向量数量积求点面距.
解:(1)法一:长方体![]() 中,因为点
中,因为点![]() 在棱
在棱![]() 上移动,
上移动,
所以![]() 平面
平面![]() ,从而
,从而![]() 为直线
为直线![]() 与平面
与平面![]() 所成的平面角,
所成的平面角,
![]() 中,
中,![]()
![]() .
.
法二:以![]() 为坐标原点,射线
为坐标原点,射线![]() 依次为
依次为![]() 轴轴,建立空间直角坐标系,则点
轴轴,建立空间直角坐标系,则点![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,设
,设![]() ,得
,得![]() ,由
,由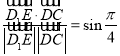 ,得
,得![]() ,故
,故![]()
(2)以![]() 为坐标原点,射线
为坐标原点,射线![]() 依次为
依次为![]() 轴,建立空间直角坐标系,则点
轴,建立空间直角坐标系,则点![]() ,
,![]() ,
, ![]() ,
,
从而![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,由
,由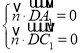
![]()
令![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为
的距离为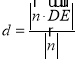
![]()

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目